Simulasi Monte Carlo

Memvisualisasikan Masalah Jarum Buffon

Bagaimana menggunakan simulasi Monte Carlo untuk menyelesaikan masalah jarum Buffon? Artikel ini akan mendemonstrasikan bagaimana memvisualisasikan dan menganimasikan simulasi Monte Carlo untuk masalah paling awal yang diajukan dan diselesaikan di Peluang Geometris, yaitu masalah jarum Buffon.
Peluang
Geometri
tutorial
Pengarang
Afiliasi

Yosep Dwi Kristanto

Pendidikan Matematika, Universitas Sanata Dharma, Yogyakarta

Terbit

October 22, 2025

Kata kunci

Hukum Bilangan Besar, kalkulus, masalah jarum Buffon, peluang empiris, peluang teoretis, simulasi Monte Carlo, trigonometri

Bayangkan kamu bermain sebuah gim. Dalam gim tersebut, kamu memiliki selembar kertas bergaris dan lidi. Panjang lidi tersebut sama dengan jarak antargaris pada kertas itu. Jika lidi tersebut dilemparkan secara acak ke kertas tersebut, kamu perlu menebak apakah lidi tersebut mengenai garis atau tidak. Jika tebakanmu benar, kamu menang. Tebakan mana yang kamu pilih?

Gim itu adalah bentuk adaptasi dari sebuah masalah paling awal yang diajukan dan diselesaikan di Peluang Geometris, masalah jarum Buffon. Masalah ini menarik karena melibatkan peluang dan geometri. Dengan demikian, kita akan memvisualisasikan masalah ini secara geometris untuk dapat melihat berapa peluangnya. Untuk melakukannya, kita menggunakan simulasi Monte Carlo.

Simulasi Monte Carlo

Simulasi Monte Carlo, atau sering dikenal dengan metode Monte Carlo, merupakan sebuah teknik matematis yang digunakan untuk memperkirakan kemungkinan luaran dari kejadian yang tak pasti. Dengan demikian, kita dapat menggunakan simulasi ini terhadap masalah jarum Buffon. Tujuannya beberapa hal, yaitu untuk:

  • membandingkan banyaknya jarum yang memotong garis dan yang tidak dalam sebuah eksperimen;

  • menggunakan Hukum Bilangan Besar dan peluang empiris untuk memperkirakan peluang kejadian mendapatkan jarum yang memotong garis;

  • memperkirakan nilai pi (\(\pi\)).

Selanjutnya, mari kita melakukan tujuan-tujuan tersebut pada bagian berikutnya.

Simulasi Masalah Jarum Buffon

Kita menggunakan pemrograman R untuk mensimulasikan masalah jarum Buffon. Untuk melakukannya, kita memanfaatkan empat paket, yaitu {tidyverse}, {scales}, {gganimate}, dan {magick}. Mari terlebih dahulu kita memanggil keempat paket tersebut.

Kode 
1library(tidyverse)
2library(scales)
3library(gganimate)
4library(magick)
1
Kita menggunakan {tidyverse} untuk mempersiapkan data dalam mensimulasikan masalah jarum Buffon.
2
Paket {scales} kita pakai untuk mengatur skala diagram-diagram yang akan kita buat.
3
Paket {gganimate} kita gunakan untuk menganimasikan simulasi masalah jarum Buffon.
4
Kita memanfaatkan {magick} untuk menggabungkan gambar-gambar animasi ke dalam sebuah gambar animasi yang tersinkron.

Deskripsi Masalah

Masalah jarum Buffon kurang lebih deskripsinya adalah sebagai berikut.

Perhatikan selembar kertas bergaris-garis sejajar yang jarak antargaris berdekatannya \(d\) satuan dan sebuah jarum yang panjangnya \(l\), dengan \(l = d\). Jika kita melemparkan jarum tersebut pada kertas itu secara acak, berapakah peluang jarum tersebut memotong garis pada kertas itu?

Tanpa mengurangi generalisasi, kita dapat mengasumsikan bahwa garis-garis pada kertas itu adalah garis-garis yang horizontal dan jarak antargaris berdekatannya \(d=1\) satuan. Dengan demikian, panjang jarumnya \(l = d = 1\). Asumsi seperti ini akan memudahkan kita untuk mensimulasikan masalah tersebut.

Terdapat dua elemen penting dalam memvisualisasikan masalah jarum Buffon tersebut, yaitu kertas bergaris dan jarumnya. Kedua elemen tersebut dapat kita visualisasikan dengan {ggplot2}, yang merupakan bagian dari {tidyverse}. Selanjutnya, kita bahas kedua elemen tersebut pada Bagian 2.2 dan Bagian 2.3.

Selembar Kertas

Kita memilih kertas yang berukuran 10 × 10. Karena kertas ini bergaris-garis horizontal dan jarak antargaris berdekatannya 1 satuan, kita dapat memvisualisasikannya dengan menggunakan kode pada Daftar 1.

Daftar 1: Kode untuk membuat kertas bergaris
Kode 
kertas <- ggplot() + 
1  geom_hline(
    yintercept = 0:10,
    color = "gray80",
    linewidth = .5
  ) + 
2  coord_equal(
    xlim = c(0, 10),
    ylim = c(0, 10)
  ) + 
3  scale_x_continuous(
    breaks = 0:10
  ) + 
4  scale_y_continuous(
    breaks = 0:10
  ) + 
5  theme_bw() +
6  theme(
    axis.title = element_blank(),
    panel.grid = element_blank(),
    plot.margin = unit(c(.5, .5, .5, .5), "cm")
  )
1
Menggunakan geom_hline() untuk membuat garis-garis horizontal yang memotong sumbu-\(y\) di 0, 1, 2, …, 10 (yintercept = 0:10), berwarna abu-abu (color = "gray80"), dan tebalnya 0,5 (linewidth = .5).
2
Mengatur agar skala-\(x\) dan \(y\) sama, serta jendela diagramnya menampilkan \(0 \leq x \leq 10\) dan \(0\leq y \leq 10\).
3
Mengatur agar skala pada sumbu-\(x\) menampilkan 0, 1, 2, …, 10.
4
Mengatur agar skala pada sumbu-\(y\) menampilkan 0, 1, 2, …, 10.
5
Memilih tema untuk diagram, yaitu yang kita pilih adalah theme_bw().
6
Mengatur tema secara lebih lanjut: (1) tidak menampilkan judul pada semua sumbu (axis.title = element_blank()), tidak menampilkan kisi-kisi, baik horizontal maupun vertikal (panel.grid = element_blank()), dan mengatur pias atas, kanan, bawah, dan kiri (plot.margin = unit(c(.5, .5, .5, .5), "cm")).

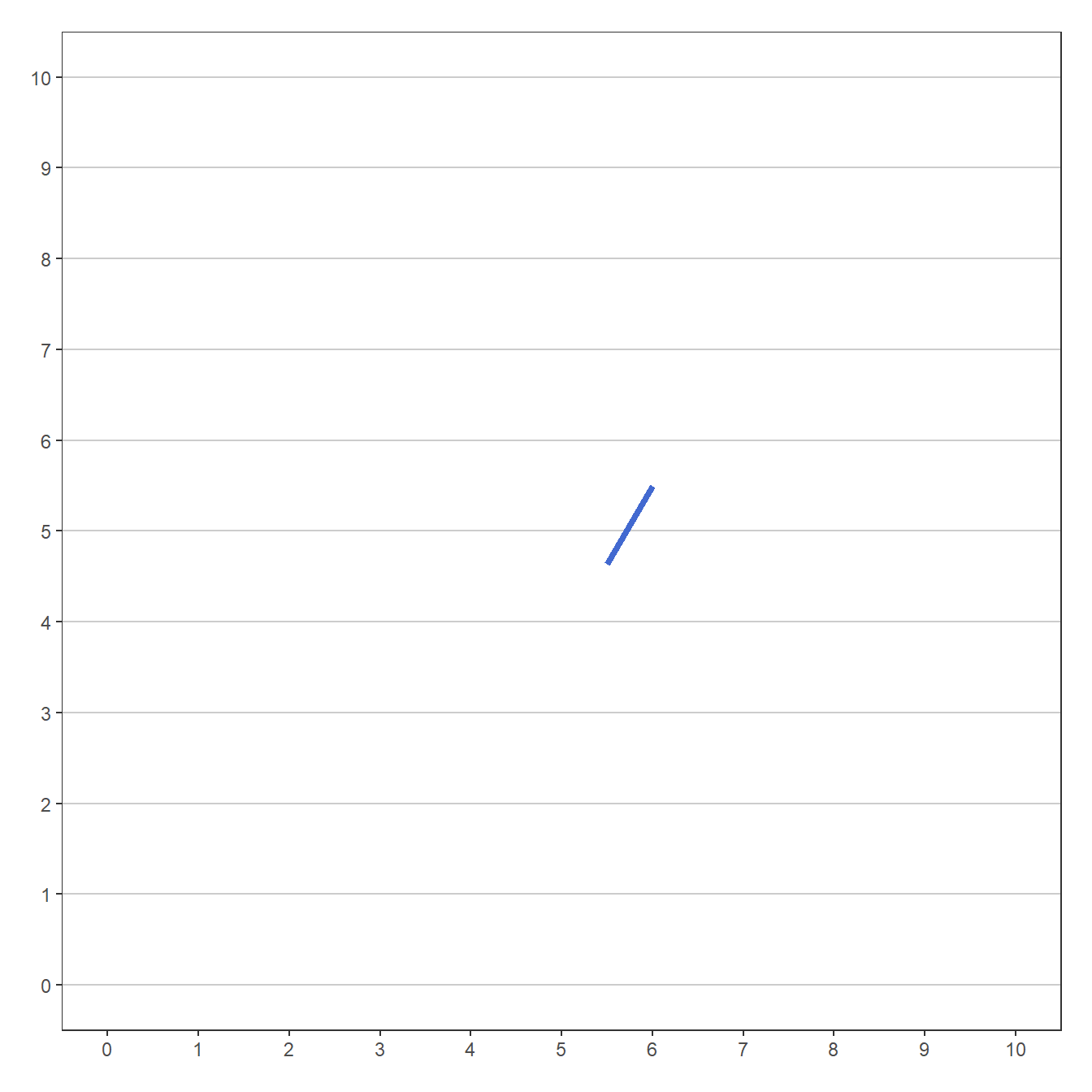
Selembar kertas yang telah kita buat ditunjukkan pada Gambar 1.

Kode 
kertas
Gambar 1: Kertas bergaris horizontal berukuran 10 × 10 yang jarak antargarisnya 1 satuan

Sebuah Jarum

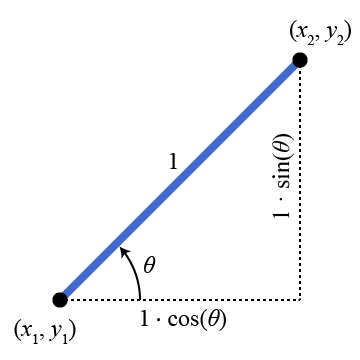
Bagaimana kita dapat membuat jarumnya? Kita dapat memvisualisasikan jarum dalam masalah ini dengan menggunakan ruas garis yang ujung-ujungnya adalah titik-titik \(\left( x_{1}, y_{1} \right)\) dan \(\left( x_{2}, y_{2} \right)\), perhatikan Gambar 2.

Gambar 2: Sebuah jarum yang direpresentasikan dengan sebuah ruas garis

Koordinat kedua ujung ruas garis tersebut saling berkaitan karena jarak keduanya haruslah \(l=1\) satuan. Jika \(\theta\) adalah besar sebuah sudut yang dibentuk oleh sebuah sinar garis horizontal ke kanan yang pangkalnya \(\left(x_{1},y_{1}\right)\) dan ruas garis tersebut, koordinat \(\left( x_{2}, y_{2} \right)\) dapat ditentukan dengan menggunakan trigonometri, seperti yang dituliskan pada Persamaan 1.

\[ \begin{matrix} x_{2}=x_{1}+1\cdot\cos\left(\theta\right)\\ y_{2}=y_{1}+1\cdot\sin\left(\theta\right) \end{matrix} \tag{1}\]

dengan \(0 \leq \theta \leq 2\pi\). Berdasarkan Persamaan 1, kita memerlukan tiga nilai, yaitu \(x_{1}\), \(y_{1}\), dan \(\theta\), untuk membuat sebuah jarum pada kertas. Sebagai contoh, untuk \(x_{1}=6\), \(y_{1}=\text{5,5}\), dan \(\theta=\frac{4}{3}\pi\), jarumnya dapat dibuat dengan menggunakan kode pada Daftar 2.

Daftar 2: Membuat sebuah jarum dengan \(x_{1}=6\), \(y_{1}=\text{5,5}\), dan \(\theta=\frac{4}{3}\pi\)
Kode 
1x_1 <- 6
y_1 <- 5.5
t_heta <- 4 / 3 * pi

2x_2 <- x_1 + 1 * cos(t_heta)
y_2 <- y_1 + 1 * sin(t_heta)

contoh_jarum <- ggplot() + 
  geom_hline(
    yintercept = 0:10,
    color = "gray80",
    linewidth = .5
  ) + 
3  annotate(
    geom = "segment",
    x = x_1, xend = x_2,
    y = y_1, yend = y_2,
    color = "#4269d0",
    linewidth = 1.5
  ) + 
  coord_equal(
    xlim = c(0, 10),
    ylim = c(0, 10)
  ) + 
  scale_x_continuous(
    breaks = 0:10
  ) + 
  scale_y_continuous(
    breaks = 0:10
  ) + 
  theme_bw() + 
  theme(
    axis.title = element_blank(),
    panel.grid = element_blank(),
    plot.margin = unit(c(.5, .5, .5, .5), "cm")
  )
1
Mendefinisikan nilai-nilai yang diketahui, yaitu x_1, y_1, dan t_heta.
2
Menghitung nilai-nilai x_2 dan y_2 berdasarkan Persamaan 1.
3
Menggunakan annotate() untuk membuat representasi sebuah jarum sebagai sebuah ruas garis (geom = "segment"), yang ujung-ujungnya di \(\left( x_{1}, y_{1} \right)\) dan \(\left( x_{2}, y_{2} \right)\) (x = x_1, xend = x_2, y = y_1, yend = y_2), berwarna biru (color = "#4269d0"), dan tebalnya 1,5 (linewidth = 1.5). Kita membuat ruas garis dengan annotate() karena ruas garis tersebut tidak tergantung dari data, tetapi kita sediakan nilai-nilai untuk x, y, xend, dan yend secara manual.

Jarum yang dihasilkan dari kode pada Daftar 2 ditunjukkan pada Gambar 3.

Kode 
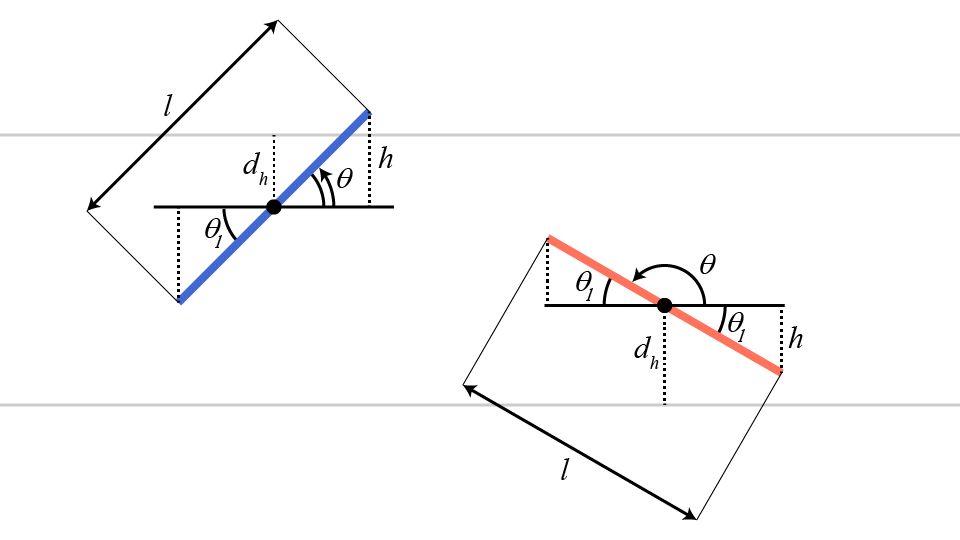
contoh_jarum
Gambar 3: Sebuah jarum dengan \(x_{1}=6\), \(y_{1}=\text{5,5}\), dan \(\theta=\frac{4}{3}\pi\)

Gambar 3 memperlihatkan secara jelas bahwa jarumnya memotong sebuah garis. Namun bagaimana kita dapat mengetahui apakah sembarang jarum yang diketahui \(x_{1}\), \(y_{1}\), dan \(\theta\)-nya memotong garis atau tidak? Untuk menjawab pertanyaan ini, perhatikan Gambar 4.

Gambar 4: Jarum-jarum yang memotong garis dan yang tidak

Berdasarkan Gambar 4, kita dapat melihat bahwa jarum yang memotong garis pada kertas nilai \(h\)-nya lebih besar dari jarak vertikal antara titik tengah jarum tersebut dan garis terdekatnya, yaitu \(d_{h}\). Padahal, \(h=\frac{1}{2}\cdot\sin\left(\theta_{l}\right)\) degan \(\theta_{l}\) adalah sudut lancip yang dibentuk oleh jarum dan garis horizontal.

Perhatikan juga bahwa garis-garis pada kertas yang kita buat pada Daftar 1 memiliki koordinat-\(y\) yang merupakan bilangan bulat. Dengan demikian, kita mendapatkan \(d_{h}=\text{min}\left(\left | y_{t}-\left \lfloor y_{t}\right \rfloor\right |,\left | y_{t}-\left \lceil y_{t}\right \rceil\right |\right)\) dengan \(y_{t}\) adalah koordinat-\(y\) titik tengah jarum tersebut. Dengan demikian, sebuah jarum yang memotong garis memenuhi kondisi pada Persamaan 2.

\[ \frac{1}{2}\sin\left(\theta_{l}\right)\geq \text{min}\left(\left | y_{t}-\left \lfloor y_{t}\right \rfloor\right |,\left | y_{t}-\left \lceil y_{t}\right \rceil\right |\right) \tag{2}\]

Kita gunakan kondisi tersebut terhadap jarum pada Gambar 3 untuk menentukan apakah jarum tersebut memotong garis atau tidak (walaupun faktanya kita telah mengetahuinya).

Daftar 3: Menguji kondisi apakah jarumnya memotong garis 
1y_t <- (y_1 + (y_1 + sin(t_heta))) / 2
2theta_l <- abs(t_heta %% pi - pi/2)
3h <- 1 / 2 * sin(theta_l)
4d_h <- min(
  abs(y_t - floor(y_t)),
  abs(y_t - ceiling(y_t))
)

5potong_garis <- if_else(
  h >= d_h, "Memotong", "Tak memotong"
)

6potong_garis
1
Menghitung koordinat-\(y\) titik tengah jarum, dan nilainya dinamai dengan y_t.
2
Menentukan sudut lancip \(\theta_{l}\) dan hasilnya kita namai dengan theta_l.
3
Menghitung nilai \(h\).
4
Menghitung nilai \(d_{h}\) dan hasilnya dinamai dengan d_h.
5
Mendefinisikan kondisi yang telah dibahas sebelumnya, dan hasilnya dinamai dengan potong_garis.
6
Mencetak nilai potong_garis. 
[1] "Memotong"

Kita telah berhasil menggunakan kondisi di atas untuk menentukan apakah jarum pada Gambar 3 memotong garis atau tidak. Hasilnya sesuai dengan pengamatan kita tentu saja.

Eksperimen Jarum Buffon

Sampai di sini kita telah dapat membuat selembar kertas dan sebuah jarum. Kita juga telah mengetahui kondisi jarum tersebut untuk memotong garis pada kertas. Sekarang kita akan memvisualisasikan sebuah eksperimen pelemparan jarum sebanyak \(n\) kali, atau selanjutnya kita sebut sebagai eksperimen jarum Buffon. Misalnya, kita memilih \(n = 100\) kali. Setiap pelemparan tersebut kita perlu menyediakan tiga nilai, yaitu \(x_{1}\), \(y_{1}\), dan \(\theta\), secara acak. Dalam R, kita dapat menggunakan fungsi runif(). Fungsi ini akan memberikan satu atau lebih nilai acak dari distribusi seragam dengan nilai minimum dan maksimum yang diberikan.

Kita buat sebuah data dengan nama data_eksperimen untuk memuat hasil eksperimen jarum Buffon sebanyak \(n=100\) percobaan. Untuk melakukannya, kita gunakan kode pada Daftar 4.

Daftar 4: Membuat data_eksperimen yang memuat luaran setiap percobaan dalam eksperimen 
1set.seed(1234)
2palet_warna <- c(
  "#4269d0","#efb118",
  "#ff725c","#6cc5b0",
  "#3ca951","#ff8ab7",
  "#a463f2","#97bbf5",
  "#9c6b4e","#9498a0"
)

data_eksperimen <- tibble(
3  x1 = runif(100, min = 1, max = 9),
  y1 = runif(100, min = 1, max = 9),
  theta = runif(100, min = 0, max = 2 * pi)
) |> 
4  mutate(
    percobaan = row_number(),
    x2 = x1 + 1 * cos(theta),
    y2 = y1 + 1 * sin(theta),
    warna = palet_warna[(percobaan %% 10) + 1]
  )
1
Mengatur benih pengacakan agar hasilnya dapat diproduksi kembali.
2
Membuat palet warna sebagai warna setiap jarumnya.
3
Menyediakan bilangan-bilangan x1, y1, dan theta secara acak. Karena ketiga bilangan tersebut mengikuti distribusi seragam, kita menggunakan fungsi runif(). Dengan distribusi seragam ini, setiap bilangan dari nilai min sampai max memiliki kemungkinan yang sama untuk terpilih.
4
Menghitung x2 dan y2, serta membuat variabel percobaan untuk memberikan identitas terhadap setiap percobaannya dan warna untuk memberikan warna terhadap setiap jarum yang dihasilkan.

Kita dapat melihat gambaran umum data_eksperimen dengan fungsi glimpse().

Kode 
glimpse(data_eksperimen)
Rows: 100
Columns: 7
$ x1        <dbl> 1.909627, 5.978395, 5.874198, 5.987036, 7.887323, 6.122485, …
$ y1        <dbl> 1.283654, 5.520609, 3.242062, 2.633571, 2.069911, 3.605455, …
$ theta     <dbl> 4.1516438, 3.3197799, 1.9948725, 4.8245782, 3.3068938, 4.601…
$ percobaan <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 1…
$ x2        <dbl> 1.3778099, 4.9942286, 5.4627189, 6.0989896, 6.9009542, 6.011…
$ y2        <dbl> 0.4367948, 5.3433631, 4.1534815, 1.6398571, 1.9053618, 2.611…
$ warna     <chr> "#efb118", "#ff725c", "#6cc5b0", "#3ca951", "#ff8ab7", "#a46…

Kita telah memiliki data_eksperimen yang memiliki tujuh variabel dan 100 baris. Baris-baris tersebut menggambarkan hasil percobaannya.

Selanjutnya, kita akan menentukan apakah setiap percobaan dalam data_eksperimen menghasilkan jarum yang memotong garis atau tidak. Untuk melakukannya, kita menerapkan ide pada Daftar 3 untuk membuat variabel baru, yaitu potong, dalam data tersebut. Perhatikan Daftar 5!

Daftar 5: Menambahkan informasi apakah jarumnya memotong garis atau tidak 
data_eksperimen <- data_eksperimen |> 
1  mutate(
    yt = (y1 + y2) / 2,
    theta_l = abs(theta %% pi - pi/2),
    h = 1 / 2 * sin(theta_l),
    d_h = pmin(
      abs(yt - floor(yt)),
      abs(yt - ceiling(yt))
    ),
2    potong = if_else(
      h >= d_h,
      "Memotong",
      "Tak memotong"
    )
  )
1
Menggunakan ide pada Daftar 3 dengan menambahkan variabel-variabel yt, theta_l, h, d_h dan potong ke dalam data_eksperimen.
2
Variabel potong akan bernilai “Memotong” jika h >= d_h. Jika sebaliknya, variabel ini akan bernilai “Tak memotong”.

Kita cek apakah data_eksperimen saat ini telah memuat informasi jarumnya memotong garis atau tidak.

Kode 
glimpse(data_eksperimen)
Rows: 100
Columns: 12
$ x1        <dbl> 1.909627, 5.978395, 5.874198, 5.987036, 7.887323, 6.122485, …
$ y1        <dbl> 1.283654, 5.520609, 3.242062, 2.633571, 2.069911, 3.605455, …
$ theta     <dbl> 4.1516438, 3.3197799, 1.9948725, 4.8245782, 3.3068938, 4.601…
$ percobaan <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 1…
$ x2        <dbl> 1.3778099, 4.9942286, 5.4627189, 6.0989896, 6.9009542, 6.011…
$ y2        <dbl> 0.4367948, 5.3433631, 4.1534815, 1.6398571, 1.9053618, 2.611…
$ warna     <chr> "#efb118", "#ff725c", "#6cc5b0", "#3ca951", "#ff8ab7", "#a46…
$ yt        <dbl> 0.8602243, 5.4319860, 3.6977718, 2.1367138, 1.9876365, 3.108…
$ theta_l   <dbl> 0.56074517, 1.39260910, 0.42407619, 0.11218922, 1.40549519, …
$ h         <dbl> 0.26590870, 0.49208331, 0.20573949, 0.05597701, 0.49318442, …
$ d_h       <dbl> 0.13977571, 0.43198600, 0.30222817, 0.13671384, 0.01236349, …
$ potong    <chr> "Memotong", "Memotong", "Tak memotong", "Tak memotong", "Mem…

Data yang kita miliki telah memuat informasi yang kita perlukan. Kita dapat melakukan analisis sederhana terhadap data_eksperimen tersebut. Misalnya, kita dapat melihat berapa jarum yang memotong garis dan yang tidak dengan kode pada Daftar 6.

Daftar 6: Menghitung banyak jarum yang memotong garis dan yang tidak
Kode 
data_eksperimen |> 
  group_by(potong) |> 
  summarise(
    frekuensi = n()
  )
# A tibble: 2 × 2
  potong       frekuensi
  <chr>            <int>
1 Memotong            60
2 Tak memotong        40

Visualisasi Hasil Eksperimen

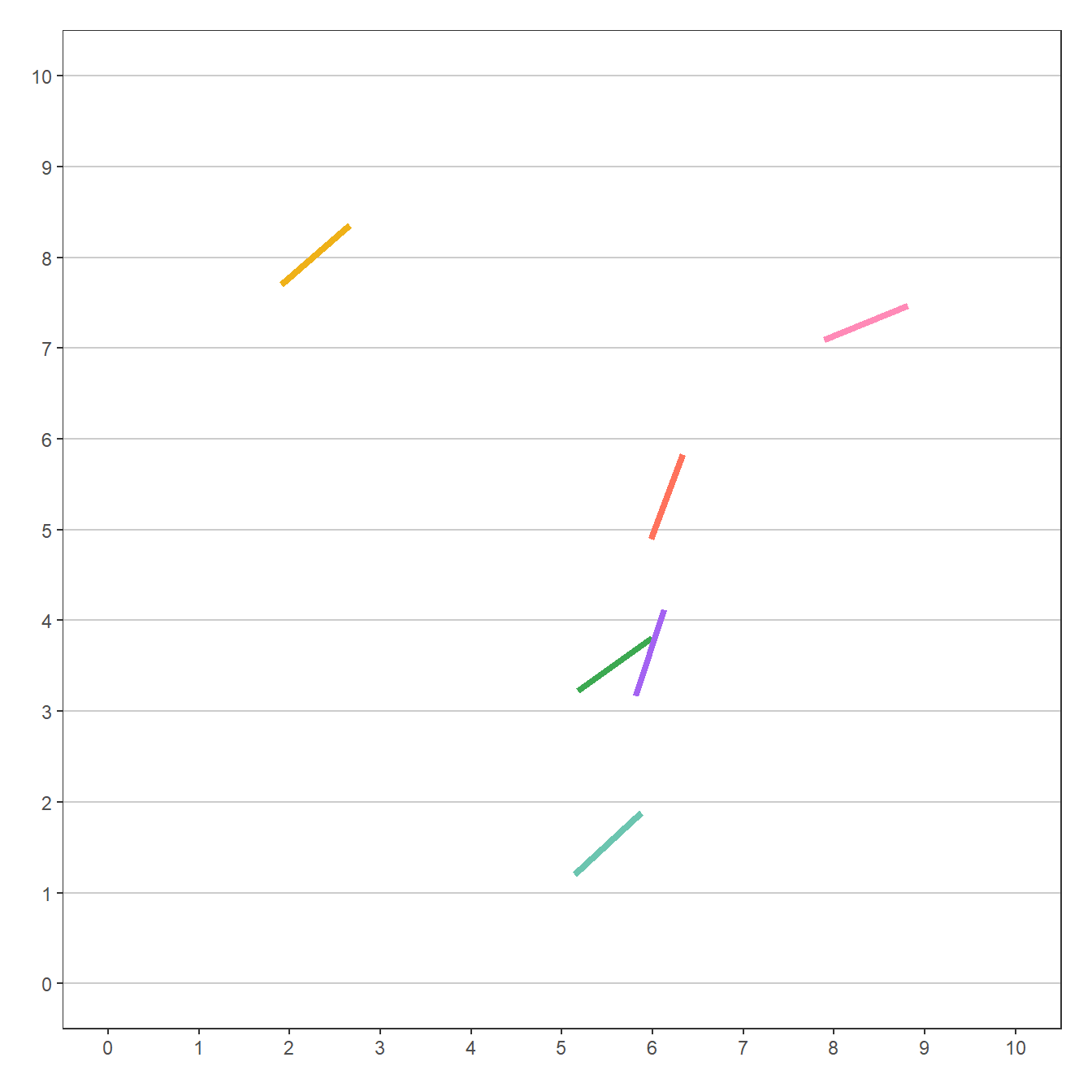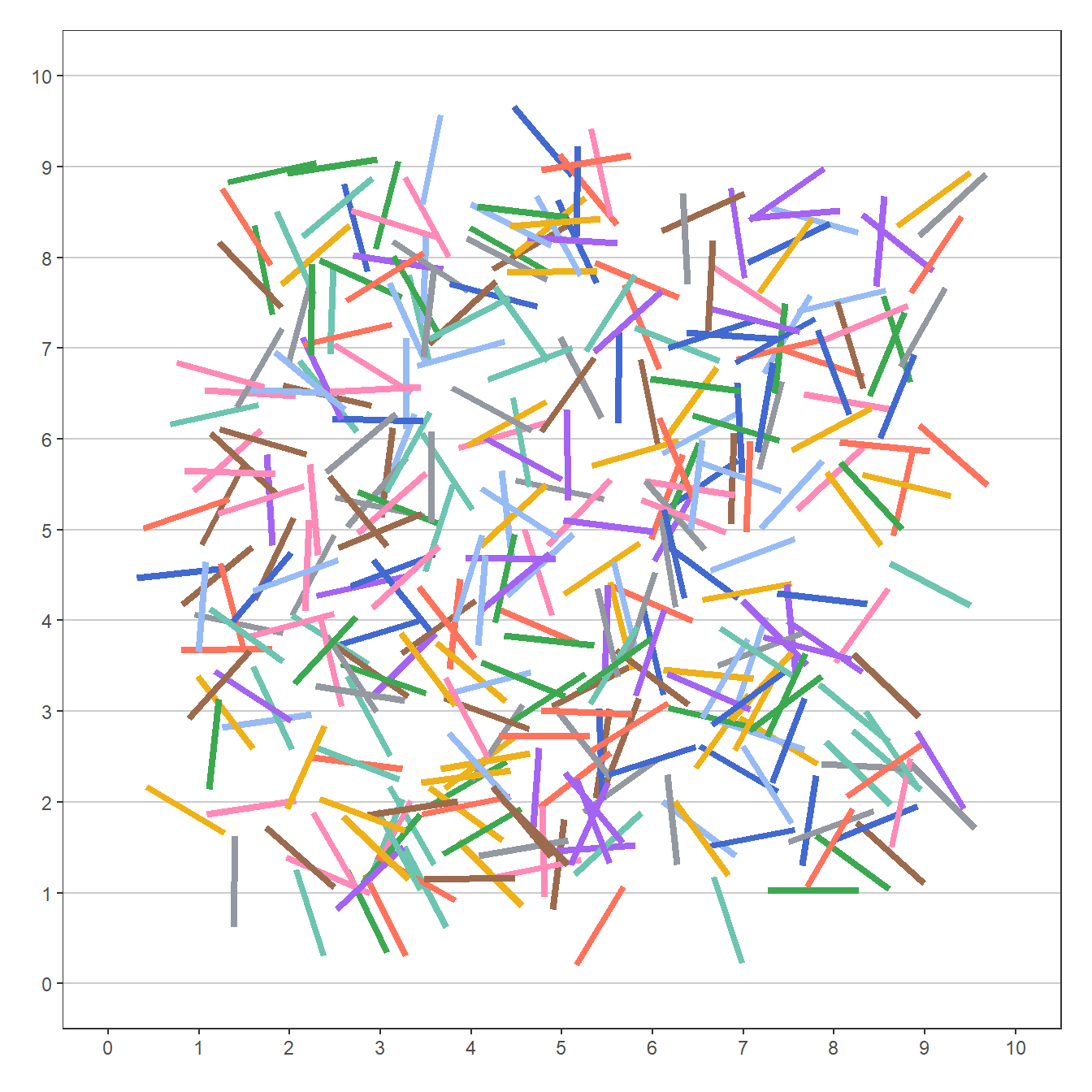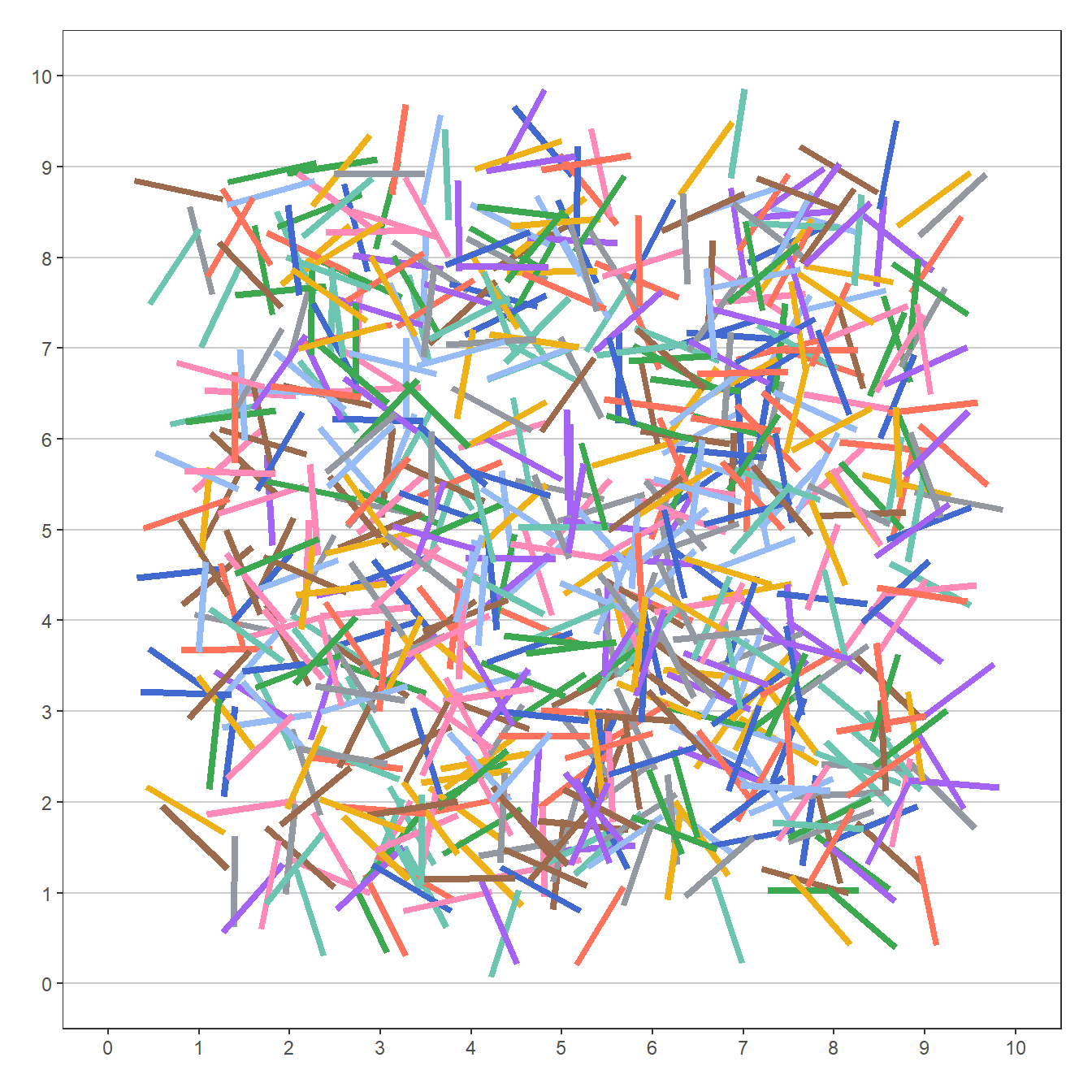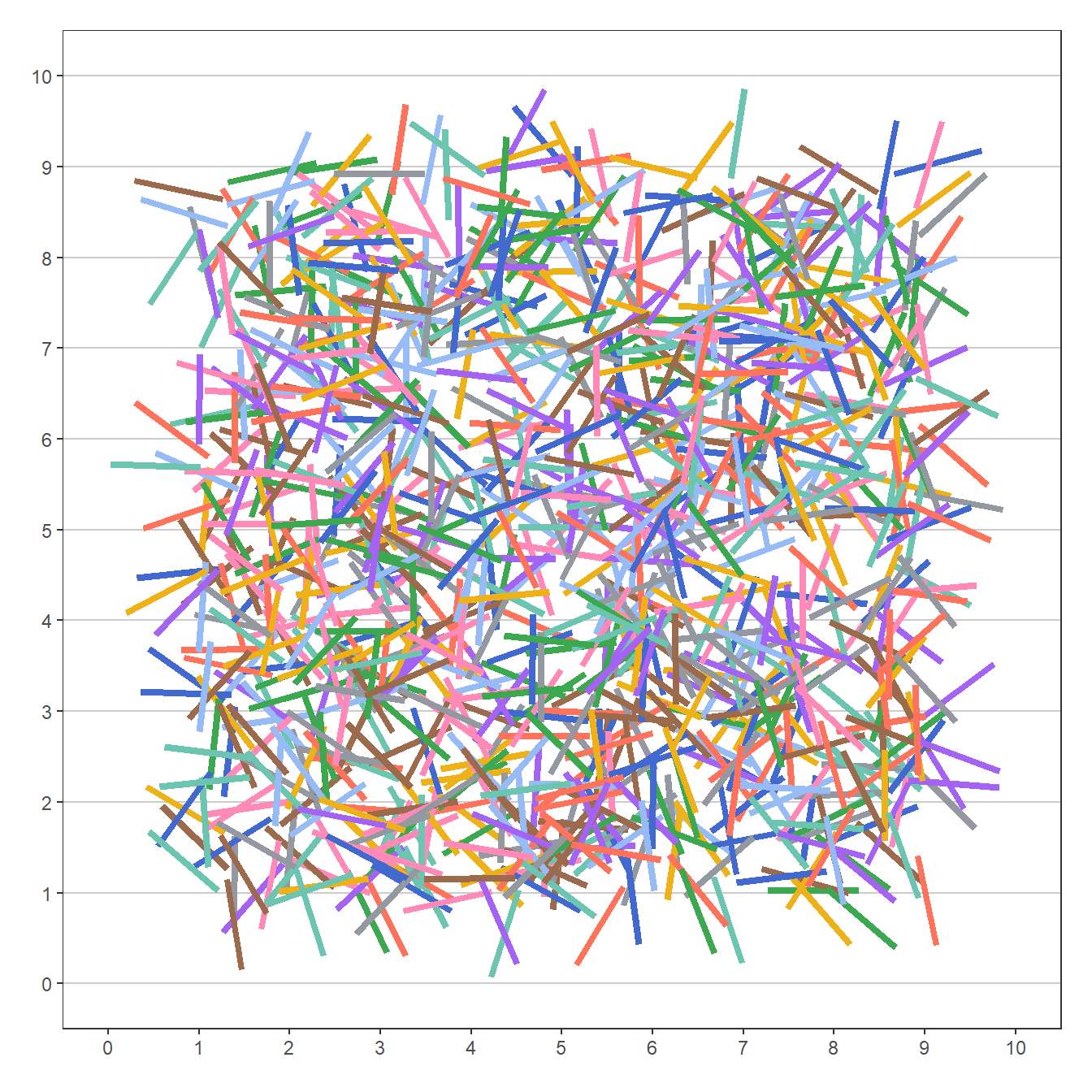
Kita dapat memvisualisasikan hasil 100 percobaan dalam data_eksperimen. Dengan menggunakan x1, y1, x2, dan y2, kita dapat menggambarkan jarum yang dihasilkan oleh setiap percobaan. Kita dapat melakukannya dengan kode pada Daftar 7.

Daftar 7: Memvisualisasikan setiap luaran dalam eksperimen
Kode 
hasil_eksperimen <- data_eksperimen |> 
  ggplot() + 
  geom_hline(
    yintercept = 0:10,
    color = "gray80",
    linewidth = 0.5
  ) + 
1  geom_segment(
    aes(
      x = x1, y = y1,
      xend = x2, yend = y2,
      color = warna
    ),
    linewidth = 1.5
  ) + 
  coord_equal(
    xlim = c(0, 10),
    ylim = c(0, 10)
  ) + 
  scale_x_continuous(
    breaks = 0:10
  ) + 
  scale_y_continuous(
    breaks = 0:10
  ) + 
2  scale_color_identity() +
  theme_bw() + 
  theme(
    legend.position = "none",
    axis.title = element_blank(),
    panel.grid = element_blank(),
    plot.margin = unit(c(.5, .5, .5, .5), "cm")
  )
1
Berbeda dengan yang kita lakukan pada Daftar 2, kita sekarang menggunakan geom_segment() untuk membuat ruas-ruas garis. Hal ini dikarenakan kita membuat ruas-ruas garis tersebut berdasarkan setiap baris dalam data_eksperimen.
2
Kita menggunakan scale_color_identity() karena kita ingin agar pemetaan kita pada geom_segment() tentang warna, yaitu color = warna, bernilai persis sama dengan nilai variabel warna-nya (tanpa melalui penskalaan).

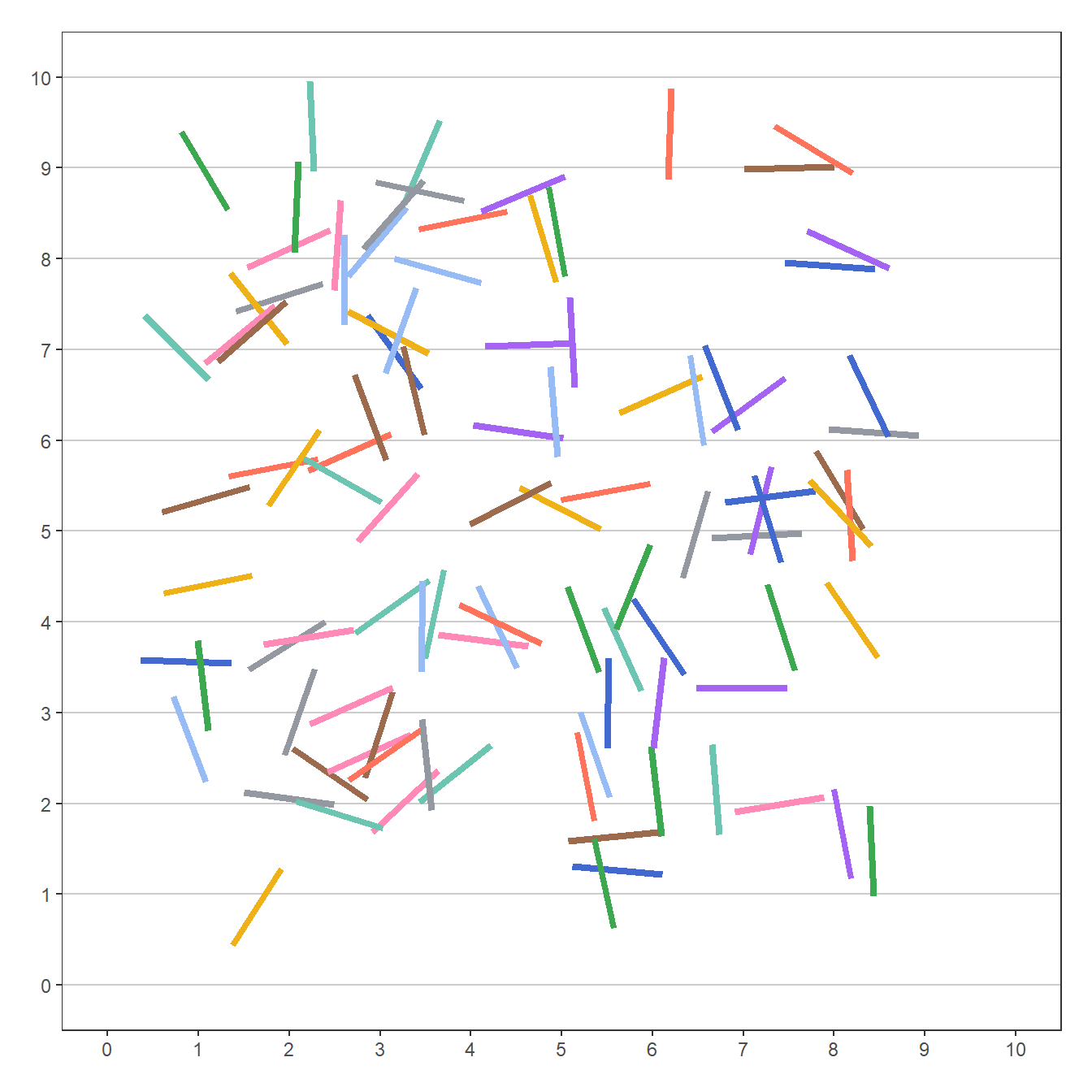
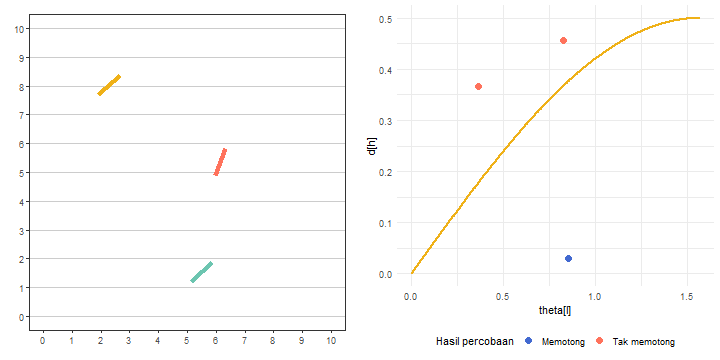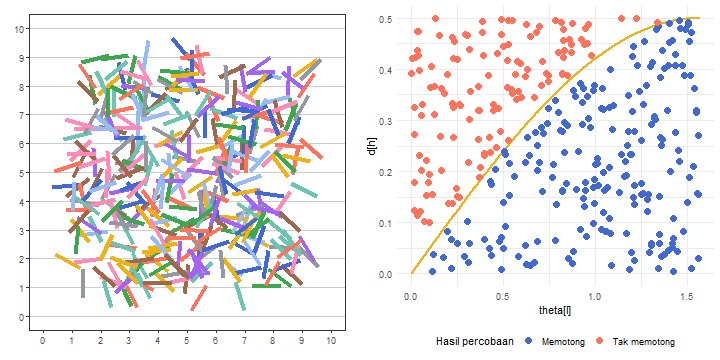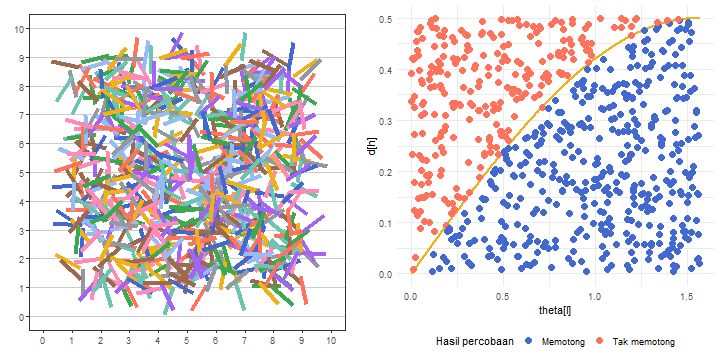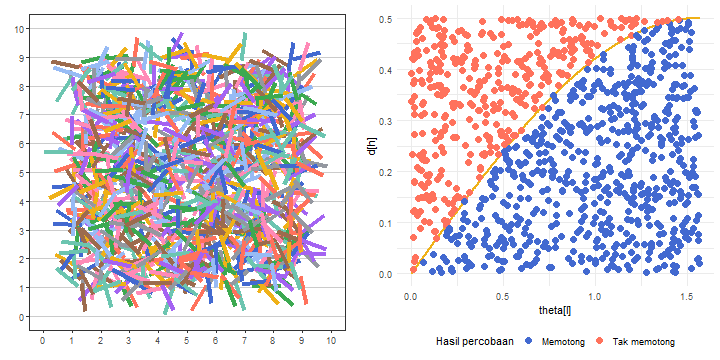
Visualisasi luaran 100 percobaan eksperimen jarum Buffon yang dihasilkan dari Daftar 7, ditunjukkan pada Gambar 5.

Kode 
hasil_eksperimen
Gambar 5: Hasil pelemparan secara acak 100 jarum pada selembar kertas

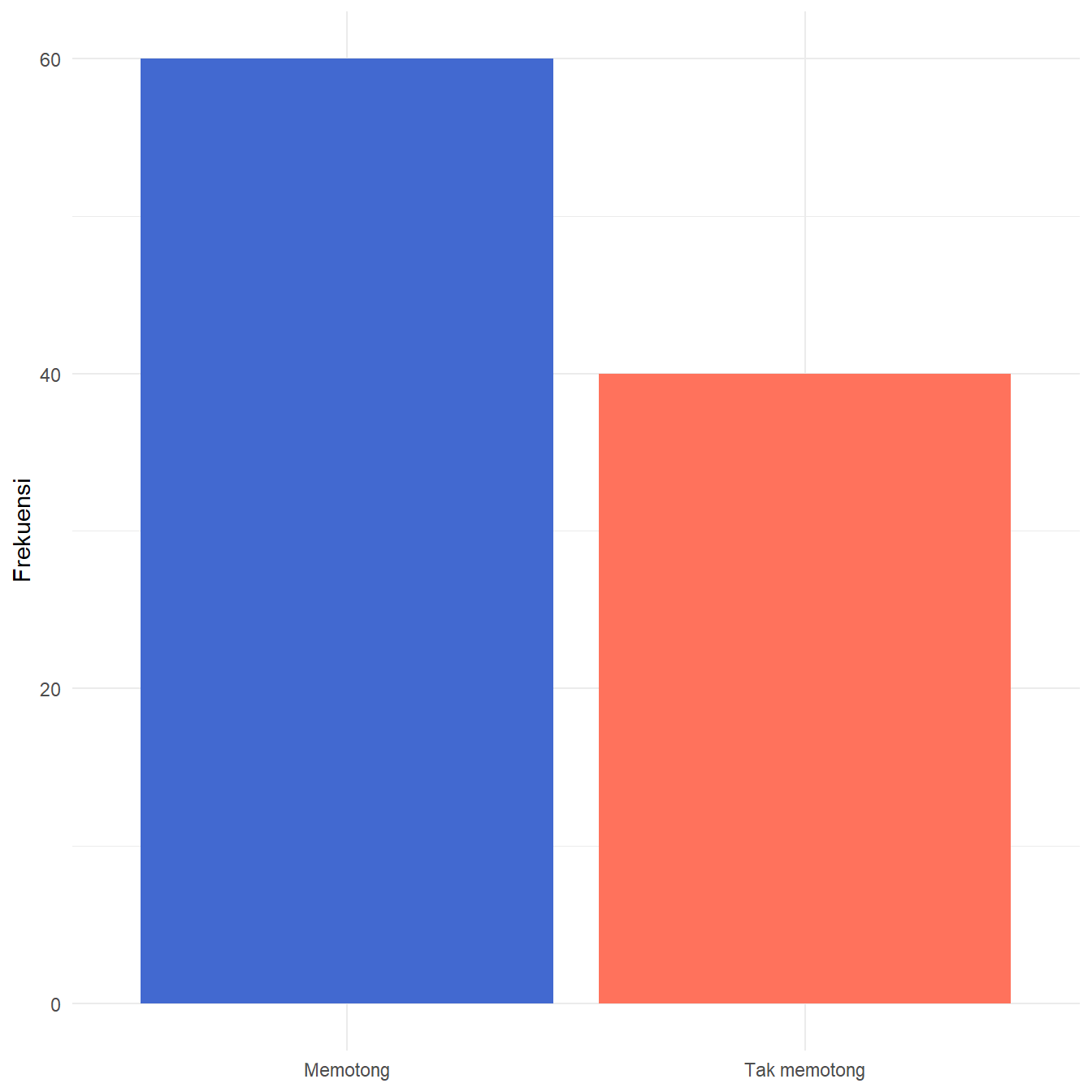
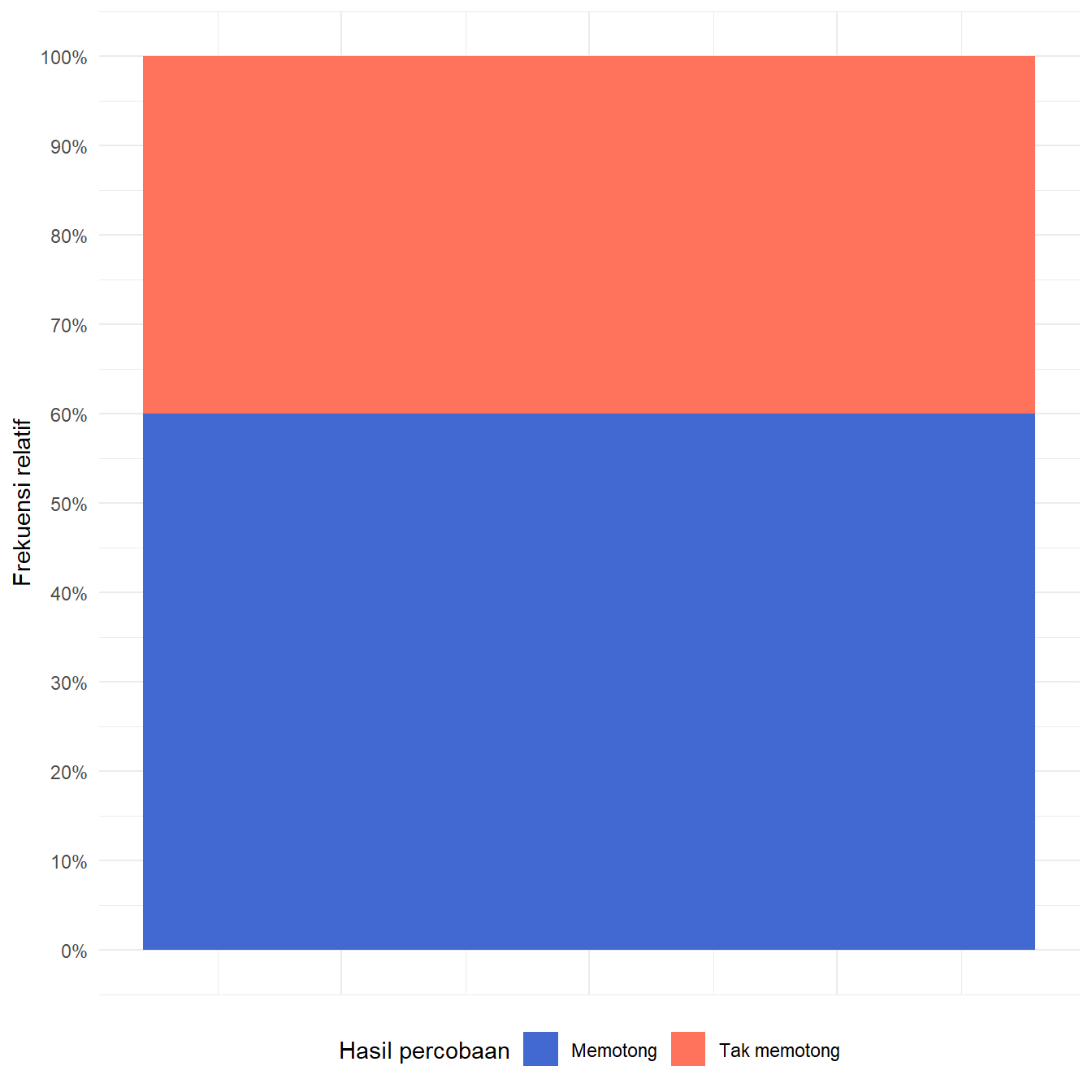
Sebelumnya kita telah mengetahui berapa banyak jarum yang memotong garis dan yang tidak. Kita juga dapat mengetahui persentasenya juga. Kedua informasi ini dapat kita visualisasikan, seperti yang disajikan pada Gambar 6!

Kode 
data_eksperimen |> 
  ggplot(aes(x = potong, fill = potong)) + 
  geom_bar() + 
  scale_fill_manual(
    values = c(
      "Memotong" = "#4269d0",
      "Tak memotong" = "#ff725c"
    )
  ) + 
  theme_minimal() + 
  theme(
    legend.position = "none",
    axis.title.x = element_blank()
  ) + 
  labs(
    y = "Frekuensi"
  )

data_eksperimen |> 
  mutate(
    potong = factor(potong, levels = c("Tak memotong", "Memotong"))
  ) |> 
  ggplot(aes(x = 1, fill = potong)) + 
  geom_bar(position = "fill") + 
  scale_y_continuous(
    labels = percent_format(),
    breaks = seq(from = 0, to = 1, by = .1)
  ) + 
  scale_fill_manual(
    values = c(
      "Tak memotong" = "#ff725c",
      "Memotong" = "#4269d0"
    ),
    name = "Hasil percobaan",
    breaks = c("Memotong", "Tak memotong")
  ) + 
  theme_minimal() + 
  theme(
    legend.position = "bottom",
    axis.title.x = element_blank(),
    axis.text.x = element_blank()
  ) + 
  labs(
    y = "Frekuensi relatif"
  )
(a) Frekuensi hasil setiap percobaan: Memotong dan Tak memotong
(b) Frekuensi relatif hasil setiap percobaan
Gambar 6: Hasil eksperimen jarum Buffon

Berdasarkan Gambar 6 (b), kita dapat mengetahui bahwa peluang empiris jarumnya memotong garis adalah 60% atau 0,6. Bagaimana dengan peluang empirisnya pada percobaan pertama, kedua, ketiga, dan seterusnya sampai ke-100? Untuk itu, kita hitung terlebih dahulu peluang empirisnya untuk setiap percobaannya dengan menggunakan kode pada Daftar 8.

Daftar 8: Menghitung peluang empiris untuk setiap percobaan 
data_eksperimen <- data_eksperimen |> 
1  mutate(
    potong_numerik = if_else(
      potong == "Memotong", 1, 0
    ),
2    peluang_empiris = cumsum(potong_numerik) / percobaan
  )

glimpse(data_eksperimen)
1
Kita tambahkan variabel potong_numerik yang nilainya 1 jika variabel potong bernilai “Memotong”, dan nilainya 0 jika potong bernilai “Tak memotong”.
2
Kita hitung peluang empiris memperoleh jarum yang memotong garis. 
Rows: 100
Columns: 14
$ x1              <dbl> 1.909627, 5.978395, 5.874198, 5.987036, 7.887323, 6.12…
$ y1              <dbl> 1.283654, 5.520609, 3.242062, 2.633571, 2.069911, 3.60…
$ theta           <dbl> 4.1516438, 3.3197799, 1.9948725, 4.8245782, 3.3068938,…
$ percobaan       <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,…
$ x2              <dbl> 1.3778099, 4.9942286, 5.4627189, 6.0989896, 6.9009542,…
$ y2              <dbl> 0.4367948, 5.3433631, 4.1534815, 1.6398571, 1.9053618,…
$ warna           <chr> "#efb118", "#ff725c", "#6cc5b0", "#3ca951", "#ff8ab7",…
$ yt              <dbl> 0.8602243, 5.4319860, 3.6977718, 2.1367138, 1.9876365,…
$ theta_l         <dbl> 0.56074517, 1.39260910, 0.42407619, 0.11218922, 1.4054…
$ h               <dbl> 0.26590870, 0.49208331, 0.20573949, 0.05597701, 0.4931…
$ d_h             <dbl> 0.13977571, 0.43198600, 0.30222817, 0.13671384, 0.0123…
$ potong          <chr> "Memotong", "Memotong", "Tak memotong", "Tak memotong"…
$ potong_numerik  <dbl> 1, 1, 0, 0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 0, …
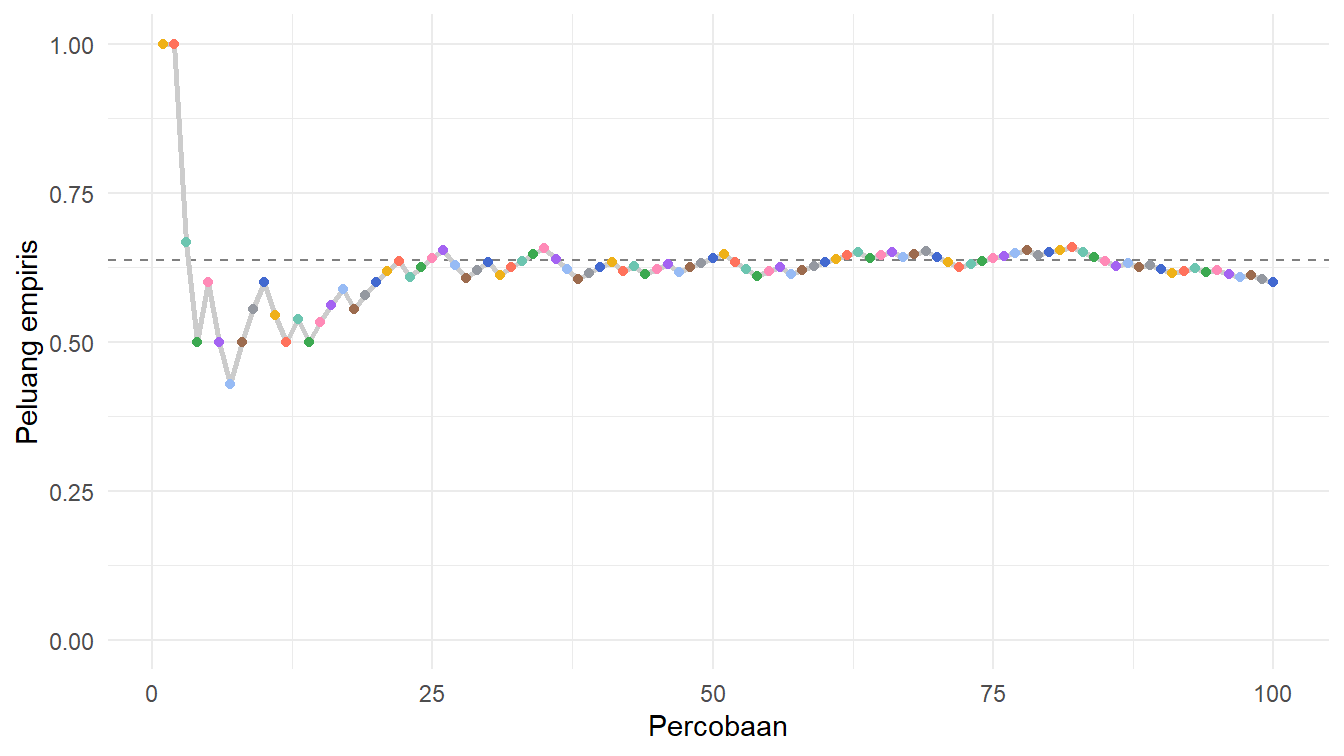
$ peluang_empiris <dbl> 1.0000000, 1.0000000, 0.6666667, 0.5000000, 0.6000000,…

Sekarang, kita dapat memvisualisaikan perubahan peluang empirisnya dari satu percobaan ke percobaan lainnya. Visualisasi semacam ini akan lebih membantu jika kita juga menambahkan peluang teoretisnya. Peluang teoretis tersebut adalah \(\frac{2}{\pi}\). Nanti kamu dapat melihat pembahasan tentang peluang teoretis ini pada Catatan 1. Kita gunakan informasi tersebut untuk membuat kode visualisasinya, seperti yang ditunjukkan pada Daftar 9.

Daftar 9: Membuat visualisasi tren peluang empiris
Kode 
tren_p_empiris <- data_eksperimen |> 
  ggplot(
1    aes(x = percobaan, y = peluang_empiris)
  ) + 
2  geom_hline(
    yintercept = 2 / pi,
    linetype = "dashed",
    color = "gray50"
  ) + 
3  geom_line(
    color = "gray80",
    linewidth = 1
  ) + 
4  geom_point(
    aes(color = warna)
  ) + 
5  coord_cartesian(
    ylim = c(0, 1)
  ) + 
  scale_color_identity() + 
  theme_minimal() + 
  labs(
    x = "Percobaan",
    y = "Peluang empiris"
  )
1
Kita atur pemetaan variabel-variabel dalam data ke grafik yang akan kita buat, yaitu x = percobaan, y = peluang_empiris.
2
Kita gunakan geom_hline() untuk membuat garis horizontal yang merepresentasikan peluang teoretisnya, yaitu yintercept = 2 / pi.
3
Kita gunakan geom_line() untuk membuat diagram garis yang berwarna color = "gray80" dan tebalnya linewidth = 1.
4
Kita gunakan geom_point() untuk membuat titik-titik yang merepresentasikan peluang empiris setiap percobaannya. Titik-titik ini kita atur agar warnanya color = warna agar sesuai dengan warna jarum-jarumnya.
5
Kita atur agar sumbu-\(y\)-nya menampilkan skala semua kemungkinan peluang empirisnya, yaitu mulai dari 0 sampai 1, dengan menginputkan argumen `ylim = c(0, 1) terhadap coord_cartesian().

Untuk melihat hasil Daftar 9, silakan perhatikan Gambar 7!

Kode 
tren_p_empiris
Gambar 7: Tren peluang empiris

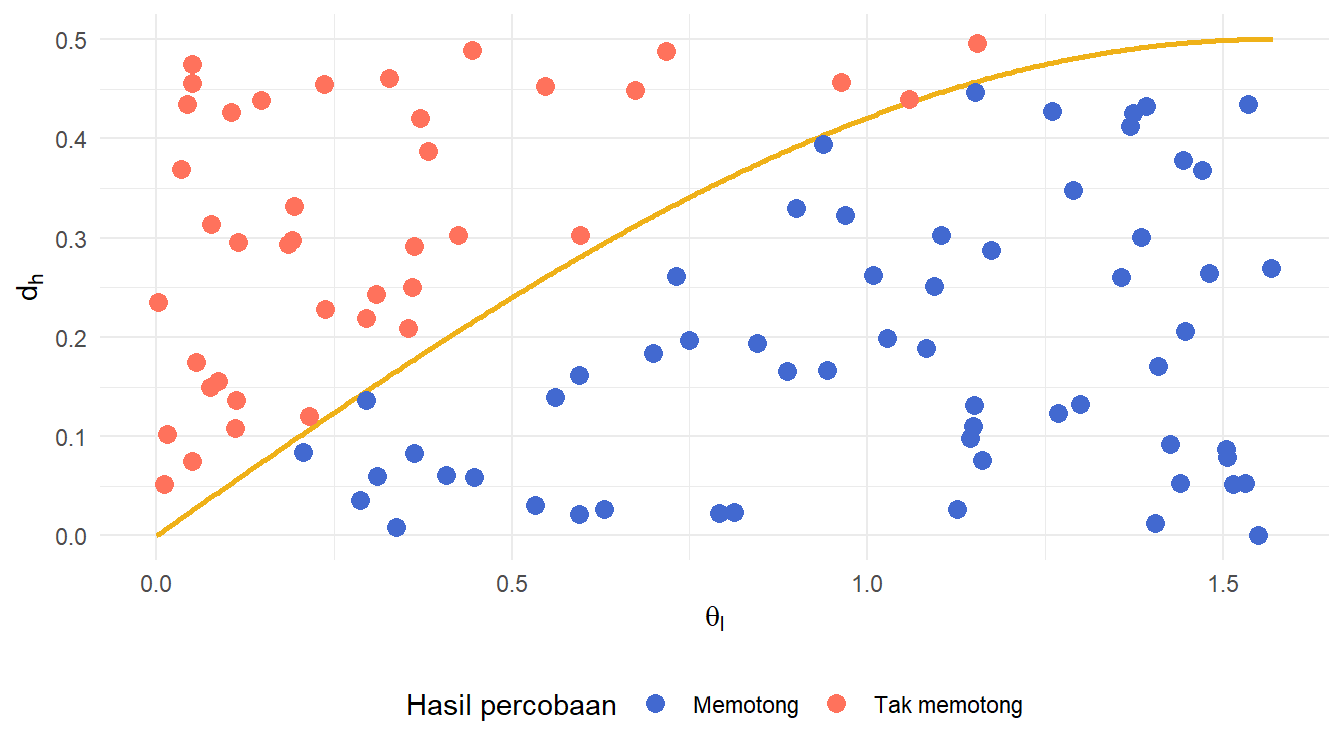
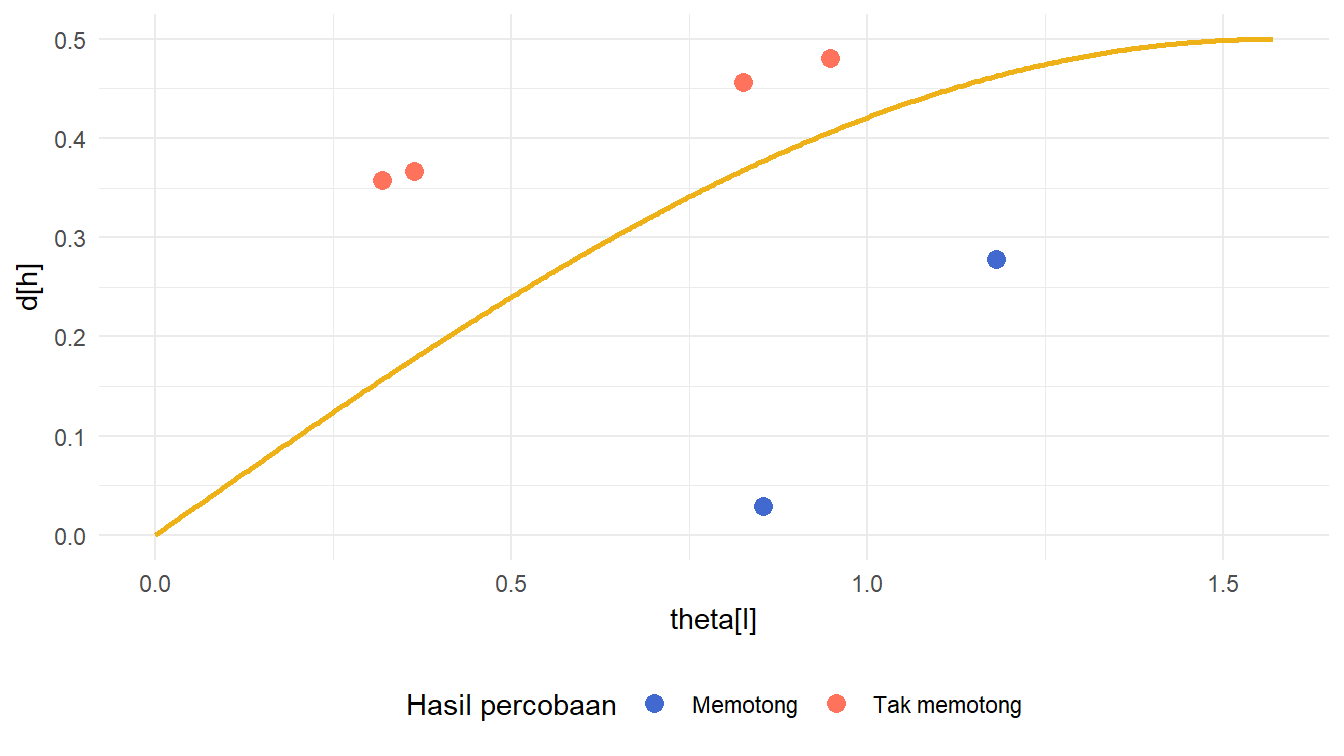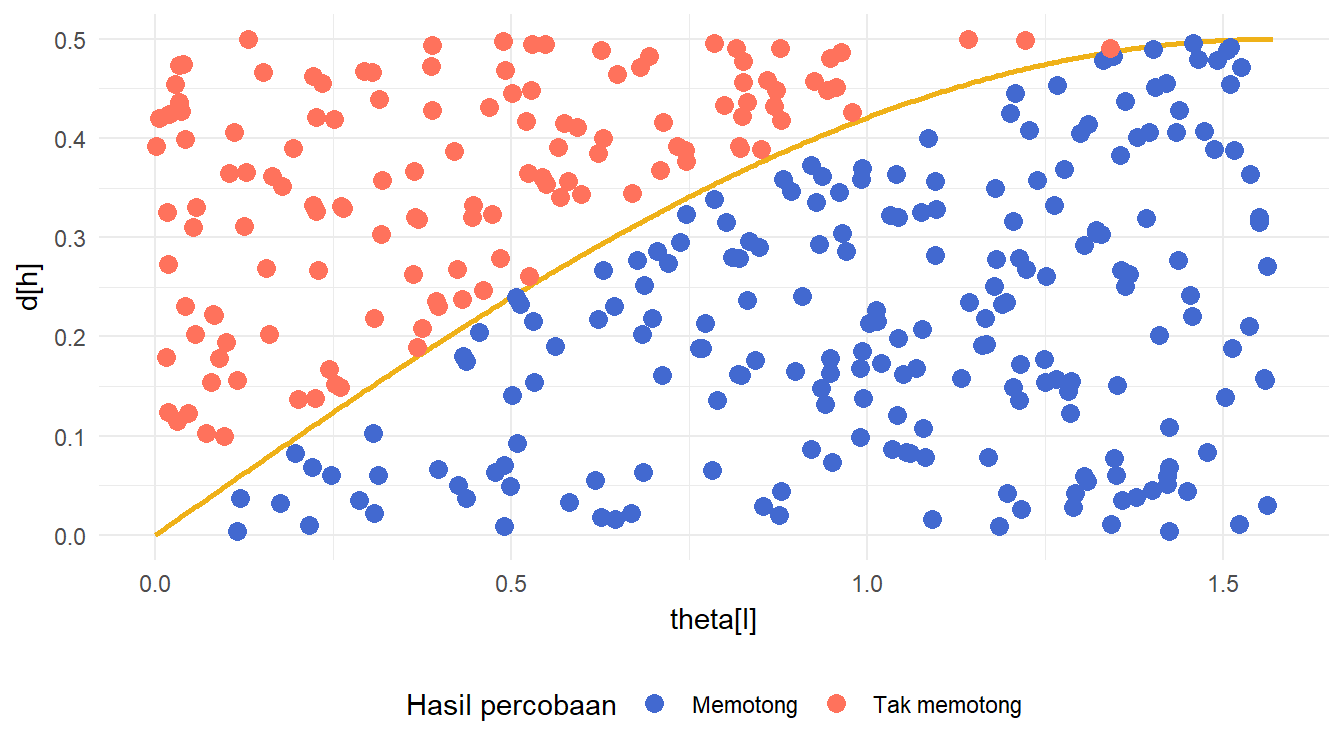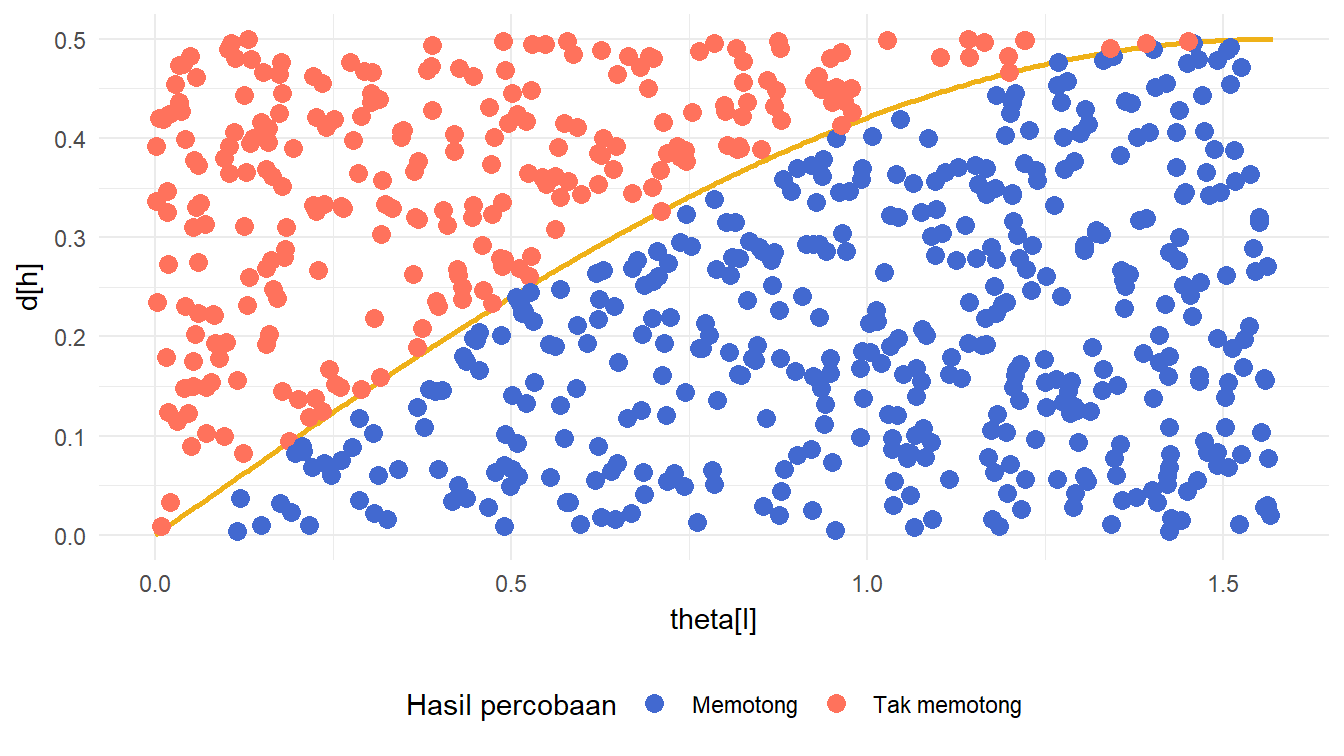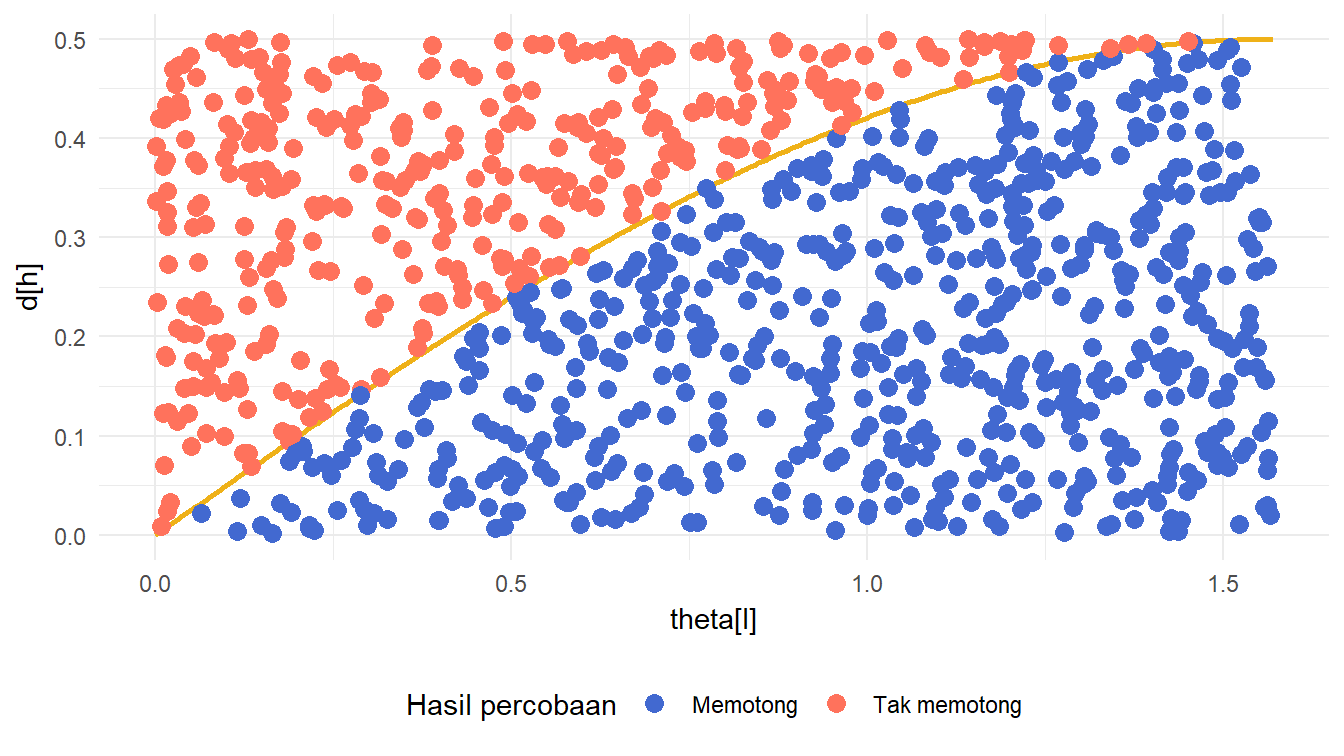
Kita juga dapat memvisualisasikan apakah setiap percobaan dalam eksperimen tersebut menghasilkan jarum yang memotong garis atau tidak dengan menggunakan Persamaan 2. Caranya, kita merepresentasikan setiap percobaan dalam eksperimen tersebut dengan titik \(\left(\theta_{l},d_{h}\right)\). Jika titik tersebut di bawah kurva \(y=\frac{1}{2}\sin\left(x\right)\), percobaannya menghasilkan jarum yang memotong garis. Kita gunakan ide seperti ini untuk membuat kode visualisasi pada Daftar 10.

Daftar 10: Memvisualisasikan hasil setiap percobaan dalam eksperimen
Kode 
1data_kurva_sin <- tibble(
  x = seq(0, pi / 2, length.out = 400)
) |> 
  mutate(y = 0.5 * sin(x))

hasil_percobaan <- data_eksperimen |> 
  ggplot(
2    aes(x = theta_l, y = d_h)
  ) +
3  geom_line(
    data = data_kurva_sin,
    aes(x = x, y = y),
    color = "#efb118",
    linewidth = 1,
    inherit.aes = FALSE
  ) + 
4  geom_point(
    aes(color = potong),
    size = 3
  ) +
5  scale_color_manual(
    values = c(
      "Memotong" = "#4269d0",
      "Tak memotong" = "#ff725c"
    ),
    name = "Hasil percobaan"
  ) +
  theme_minimal() + 
  theme(
    legend.position = "bottom"
  ) + 
  labs(
    x = expression(theta[l]),
    y = expression(d[h])
  )
1
Kita siapkan data_kurva_sin untuk selanjutnya digunakan untuk membuat kurva \(y=\frac{1}{2} \sin \left( x \right)\).
2
Kita atur pemetaan data dan diagramnya, yaitu x = theta_l, y = d_h.
3
Kita menggunakan geom_line() untuk membuat kurva sinus dengan menggunakan data_kurva_sin.
4
Kita merepresentasikan setiap percobaannya dengan titik dan menggunakan pemetaan yang kita definisikan pada nomor 2.
5
Kita mengatur warna titik-titik yang merepresentasikan jarum yang “Memotong” dan “Tak memotong”.

Dari kode pada Daftar 10, kita mendapatkan visualisasi yang disajikan pada Gambar 8.

Kode 
hasil_percobaan
Gambar 8: Hasil setiap percobaan dalam eksperimen
Catatan 1: Peluang Teoretis

Gambar 8 sangat intuitif untuk menentukan peluang teoretis kejadian mendapatkan jarum yang memotong garis pada kertas. Tentu untuk kasus kita di sini adalah \(l=1=d\) karena gambar tersebut diperoleh dari asumsi tersebut.

Perhatikan lagi Gambar 8. Apa yang terjadi jika eksperimen yang kita lakukan memuat tak hingga percobaan? Di bawah kurva \(y=\frac{1}{2}\sin\left(x\right)\) akan penuh dengan titik-titik biru, yang merepresentasikan kejadian mendapatkan jarum yang memotong garis. Secara lebih spesifik, sebanyak tak hingga titik biru tersebut akan mengisi daerah di bawah \(y=\frac{1}{2}\sin\left(x\right)\) dan di atas \(y=0\), serta di kanan \(x=0\) dan di kiri \(x=\frac{\pi}{2}\).

Padahal, semua kemungkinan posisi titik-titik dalam eksperimen tersebut adalah daerah di dalam persegi panjang yang dibatasi oleh \(y=\frac{1}{2}\), \(y = 0\), \(x=0\), dan \(x=\frac{\pi}{2}\). Dengan demikian, peluang teoretis mendapatkan kejadian jarum yang melewati garis sama dengan proporsi antara luas daerah yang mungkin ditempati oleh titik-titik biru dan luas daerah persegi panjang tersebut. Secara matematis, kita dapat menggunakan kalkulus untuk menentukan proporsi tersebut.

\[ \begin{aligned}P &= \frac{\displaystyle \int_{0}^{\frac{\pi}{2}} \frac{1}{2} \sin(x)\,dx}{\displaystyle \frac{\pi}{2} \cdot \frac{1}{2}} \\[6pt] &= \frac{2}{\pi} \left[ -\cos(x) \right]_{0}^{\frac{\pi}{2}} \\[6pt] &= \frac{2}{\pi} \bigl( -\cos(\tfrac{\pi}{2}) + \cos(0) \bigr) \\[6pt] &= \frac{2}{\pi}\end{aligned} \]

Dari perhitungan tersebut kita menemukan bahwa peluang teoretisnya adalah \(\frac{2}{\pi}\). Untuk kasus-kasus lainnya, yaitu untuk sembarang \(l\) dan \(d\), kamu dapat mencari ide dari laman Wikipedia atau Wolfram Mathworld, misalnya.

Membuat Simulasi Menjadi Lebih Hidup

Pada Bagian 2 kita telah memahami masalah jarum Buffon dengan simulasi Monte Carlo dan memvisualisasikan hasil eksperimennya. Kita dapat menjadikan simulasi masalah tersebut menjadi lebih hidup dengan menggunakan animasi. Teknik penggunaan animasi ini juga telah kita bahas pada pos sebelumnya. Selain itu, kita juga akan menambah banyak percobaannya menjadi \(n=1000\) kali.

Pertama yang kita lakukan adalah mempersiapkan datanya. Untuk melakukannya, kita menggunakan alur kerja yang serupa dengan yang telah kita lakukan dari Daftar 4, Daftar 5, sampai Daftar 8. Kita rangkum alur kerja tersebut untuk membuat fungsi eksperimen_buffon() pada Daftar 11.

Daftar 11: Membuat data eksperimen pelemparan jarum secara acak
Kode 
eksperimen_buffon <- function(n = 100) {
  set.seed(1234)
  palet_warna <- c(
  "#4269d0","#efb118",
  "#ff725c","#6cc5b0",
  "#3ca951","#ff8ab7",
  "#a463f2","#97bbf5",
  "#9c6b4e","#9498a0"
)   
  tibble(
    x1 = runif(n, 1, 9),
    y1 = runif(n, 1, 9),
    theta = runif(n, 0, 2 * pi),
    percobaan = 1:n
  ) |> 
    mutate(
      x2 = x1 + 1 * cos(theta),
      y2 = y1 + 1 * sin(theta),
      warna = palet_warna[(percobaan %% length(palet_warna)) + 1],
      yt = (y1 + y2) / 2,
      theta_l = abs(theta %% pi - pi/2),
      h = 1 / 2 * sin(theta_l),
      d_h = pmin(
        abs(yt - floor(yt)),
        abs(yt - ceiling(yt))
      ),
      potong = if_else(
        h >= d_h, "Memotong", "Tak memotong"
      ),
      potong_numerik = if_else(
      potong == "Memotong", 1, 0
    ),
    peluang_empiris = cumsum(potong_numerik) / percobaan
    )
}

Fungsi eksperimen_buffon() dapat kita gunakan untuk membuat data hasil eksperimen masalah jarum Buffon dengan input n, yaitu banyaknya percobaan dalam eksperimen tersebut. Dengan demikian, jika kita ingin membuat data_eksperimen yang memuat \(n=1000\) percobaan, kita manfaatkan fungsi tersebut seperti pada Daftar 12.

Daftar 12: Membuat data_eksperimen dengan 1000 percobaan
Kode 
data_eksperimen <- eksperimen_buffon(1000)

Untuk melihat secara sekilas hasil eksperimen yang dimuat dalam data_eksperimen tersebut, kita dapat menggunakan glimpse().

Kode 
glimpse(data_eksperimen)
Rows: 1,000
Columns: 14
$ x1              <dbl> 1.909627, 5.978395, 5.874198, 5.987036, 7.887323, 6.12…
$ y1              <dbl> 7.701071, 4.899730, 1.882696, 3.810904, 7.088504, 4.11…
$ theta           <dbl> 0.7165175, 1.2076797, 3.8859660, 3.7640007, 0.3888313,…
$ percobaan       <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,…
$ x2              <dbl> 2.6637247, 6.3335846, 5.1386852, 5.1745586, 8.8126758,…
$ y2              <dbl> 8.3578339, 5.8345244, 1.2051850, 3.2279108, 7.4676115,…
$ warna           <chr> "#efb118", "#ff725c", "#6cc5b0", "#3ca951", "#ff8ab7",…
$ yt              <dbl> 8.029453, 5.367127, 1.543940, 3.519407, 7.278058, 3.64…
$ theta_l         <dbl> 0.854278785, 0.363116599, 0.826423019, 0.948388257, 1.…
$ h               <dbl> 0.3770487226, 0.1775946664, 0.3677563190, 0.4062384624…
$ d_h             <dbl> 0.02945260, 0.36712720, 0.45605951, 0.48059253, 0.2780…
$ potong          <chr> "Memotong", "Tak memotong", "Tak memotong", "Tak memot…
$ potong_numerik  <dbl> 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 0, …
$ peluang_empiris <dbl> 1.0000000, 0.5000000, 0.3333333, 0.2500000, 0.4000000,…

Berdasarkan luaran di atas, kita dapat melihat bahwa data_eksperimen tersebut memiliki 14 variabel, mulai dari x1, y1, theta, sampai peluang_empiris. Data tersebut juga memuat 1000 baris yang setiap barisnya merupakan hasil percobaan dalam eksperimen. Dengan demikian, kita mendapatkan data_eksperimen yang kita kehendaki.

Animasi Eksperimen Jarum Buffon

Data eksperimen 1000 percobaan telah siap. Berikutnya, kita akan membuat visualisasi seperti pada Gambar 5, tetapi dengan menggunakan animasi. Dalam animasi tersebut, kita buat agar jarumnya tampak jatuh ke kertas secara bergiliran. Kita lakukan hal ini dengan kode pada Daftar 13.

Daftar 13: Menganimasikan jarum yang jatuh ke kertas
Kode 
plot_anim_jarum <- data_eksperimen |> 
  ggplot() + 
  geom_hline(
    yintercept = 0:10,
    color = "gray80",
    linewidth = 0.5
  ) + 
  geom_segment(
    aes(
      x = x1, y = y1,
      xend = x2, yend = y2,
      group = percobaan,
      color = warna
    ),
    linewidth = 1.5
  ) + 
  coord_equal(
    xlim = c(0, 10),
    ylim = c(0, 10)
  ) + 
  scale_x_continuous(
    breaks = 0:10
  ) + 
  scale_y_continuous(
    breaks = 0:10
  ) + 
  scale_color_identity() + 
  theme_bw() + 
  theme(
    legend.position = "none",
    axis.title = element_blank(),
    panel.grid = element_blank(),
    plot.margin = unit(c(.5, .5, .5, .5), "cm")
  ) + 
  transition_reveal(along = percobaan)

Sekarang kita telah memiliki objek plot_anim_jarum. Objek tersebut merupakan objek gganim yang menyajikan animasi eksperimen pelemparan jarum ke kertas. Apabila kita perhatikan kode pada Daftar 13 hampir sama persis dengan kode pada Daftar 7 untuk membuat Gambar 5. Perbedaannya hanya pada penambahan group = percobaan pada pemetaan variabel dalam geom_segment() dan transition_reveal().

Fungsi transition_reveal() merupakan fungsi dari {gganimate} yang digunakan untuk membuat animasi yang menampilkan data secara bertahap berdasarkan urutan sebuah variabel. Agar animasinya memunculkan hasil percobaan 1; 1 dan 2; 1, 2, dan 3; dan seterusnya, kita perlu menambahkan argumen along = percobaan untuk membuat animasi tersebut dimunculkan berdasarkan nilai variabel percobaan.

Selain itu, kita juga perlu menambahkan group = percobaan untuk memberitahu ggplot() agar setiap data jarum dalam satu percobaan adalah satu kelompok data sendiri. Hal ini untuk mencegah ggplot() agar tidak menyambungkan satu jarum dari suatu percobaan dengan jarum dari percobaan lainnya.

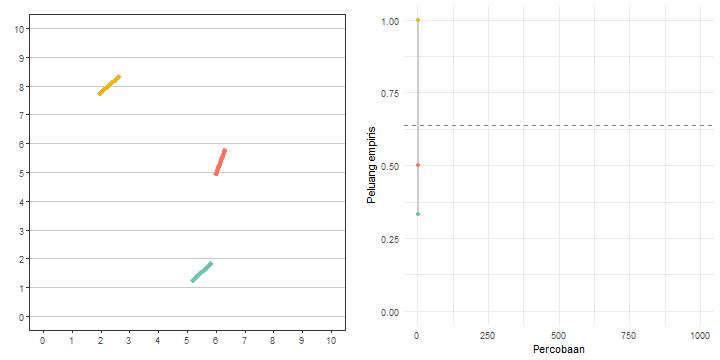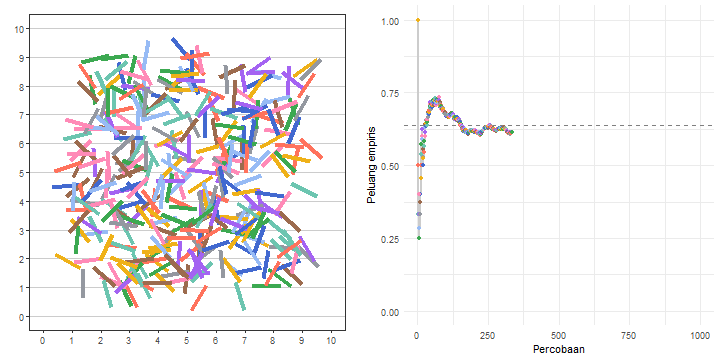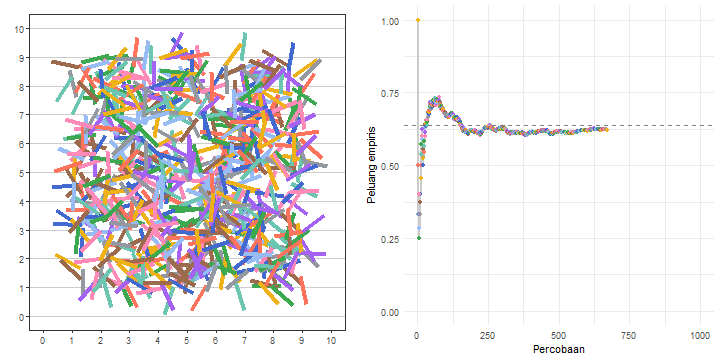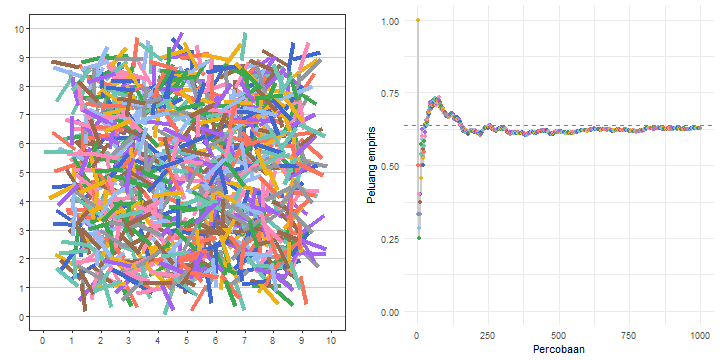
Ingin tahu bagaimana animasinya? Untuk mengetahuinya, kita cetak objek plot_anim_jarum. Hasilnya disajikan pada Gambar 9.

Kode 
plot_anim_jarum
Gambar 9: Animasi yang mengilustrasikan eksperimen masalah jarum Buffon yang memuat 1000 percobaan

Voilà! Kita telah berhasil menganimasikan eksperimen 1000 percobaan jarum Buffon.

Animasi Peluang Empiris

Kita dapat menganimasikan bagaimana perubahan peluang empiris eksperimen jarum Buffon, dari satu percobaan ke percobaan lainnya. Dengan kata lain, kita akan menganimasikan Gambar 7.

Untuk melakukannya, kita tambahkan transition_reveal(along = percobaan) terhadap kode yang membuat Gambar 7, yaitu Daftar 9. Dengan demikian, kode untuk membuat animasi tersebut ditunjukkan pada Daftar 14.

Daftar 14: Membuat animasi tren peluang empiris
Kode 
plot_anim_p_empiris <- data_eksperimen |> 
  ggplot(aes(x = percobaan, y = peluang_empiris)) + 
  geom_hline(
    yintercept = 2 / pi,
    linetype = "dashed",
    color = "gray50"
  ) + 
  geom_line(
    color = "gray80",
    linewidth = 1
  ) + 
  geom_point(
    aes(color = warna, group = percobaan)
  ) + 
  coord_cartesian(
    ylim = c(0, 1)
  ) + 
  scale_color_identity() + 
  theme_minimal() + 
  labs(
    x = "Percobaan",
    y = "Peluang empiris"
  ) + 
  transition_reveal(
    along = percobaan
  )

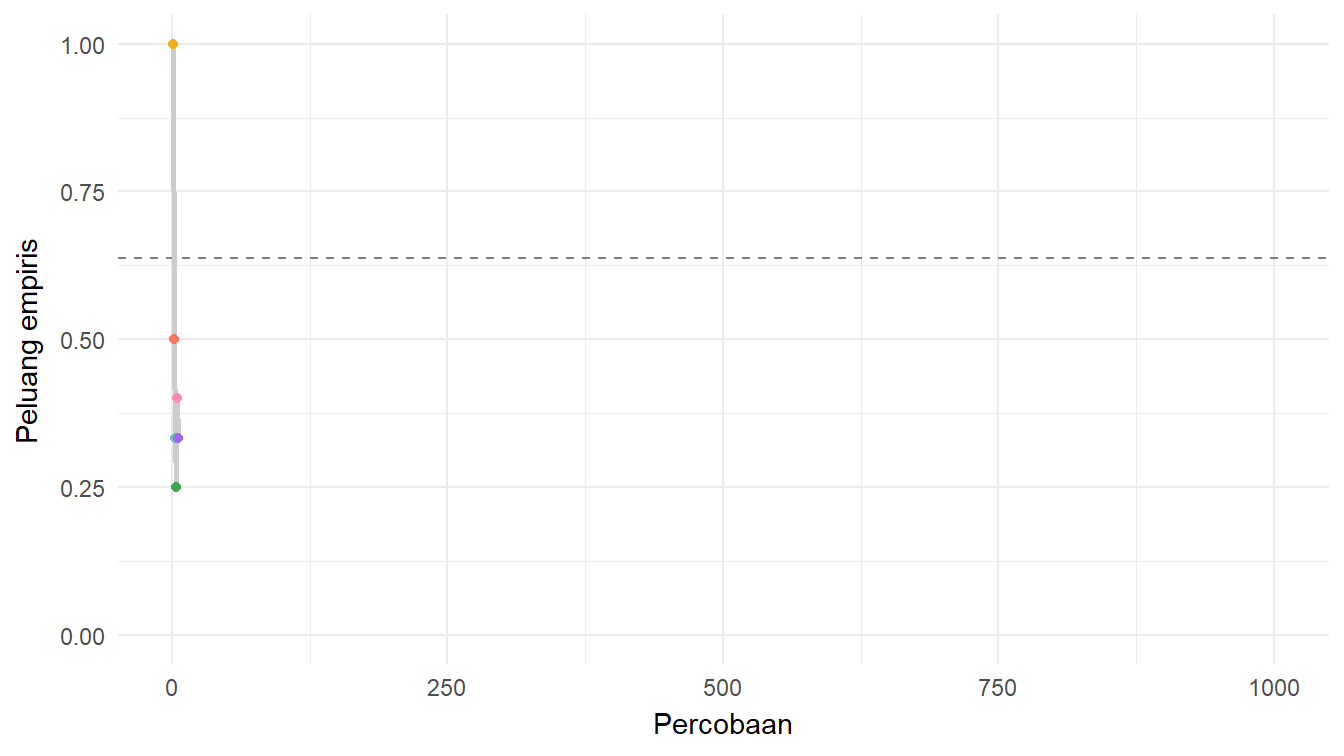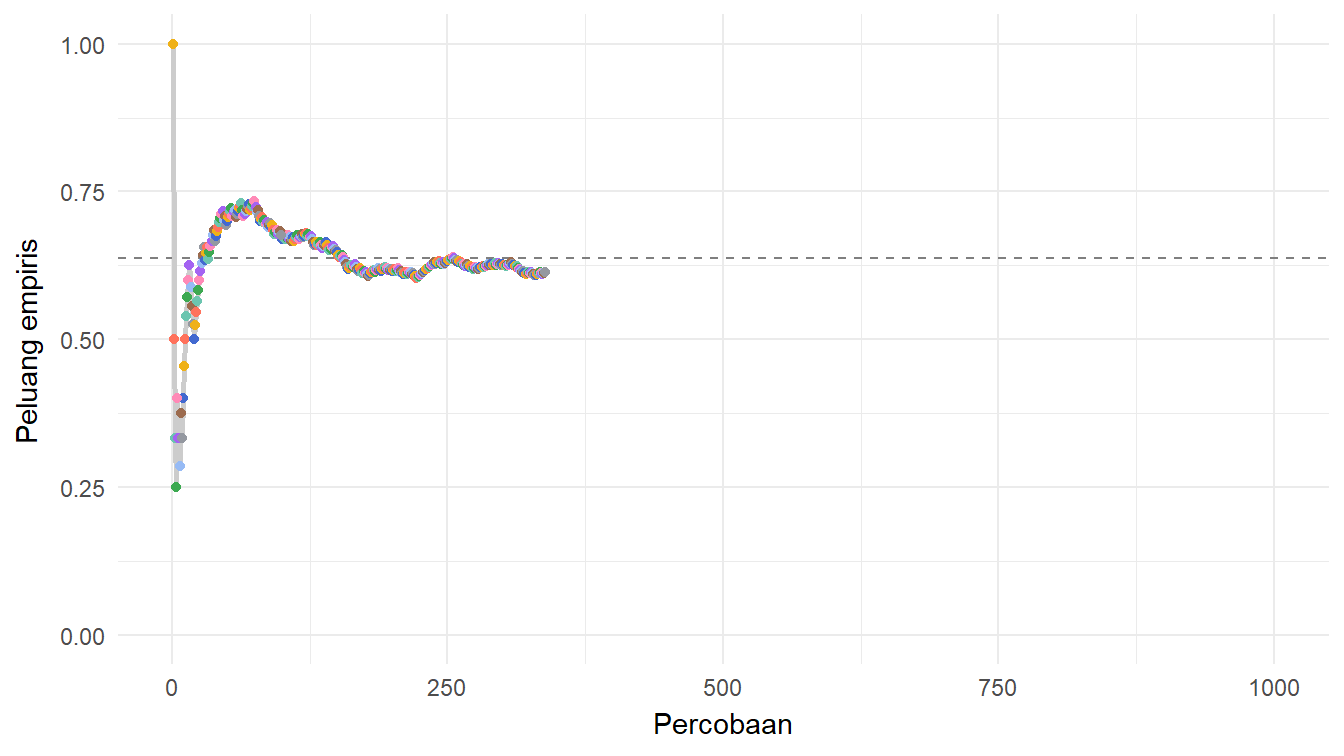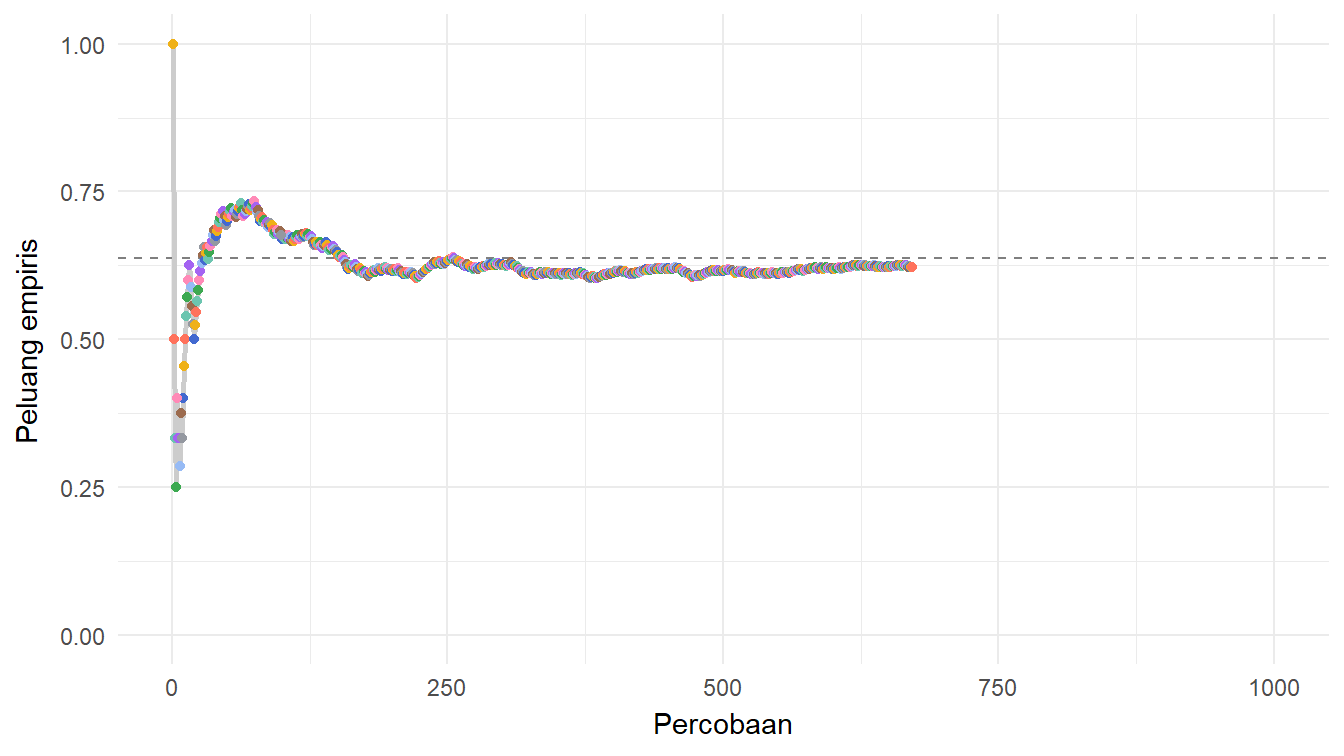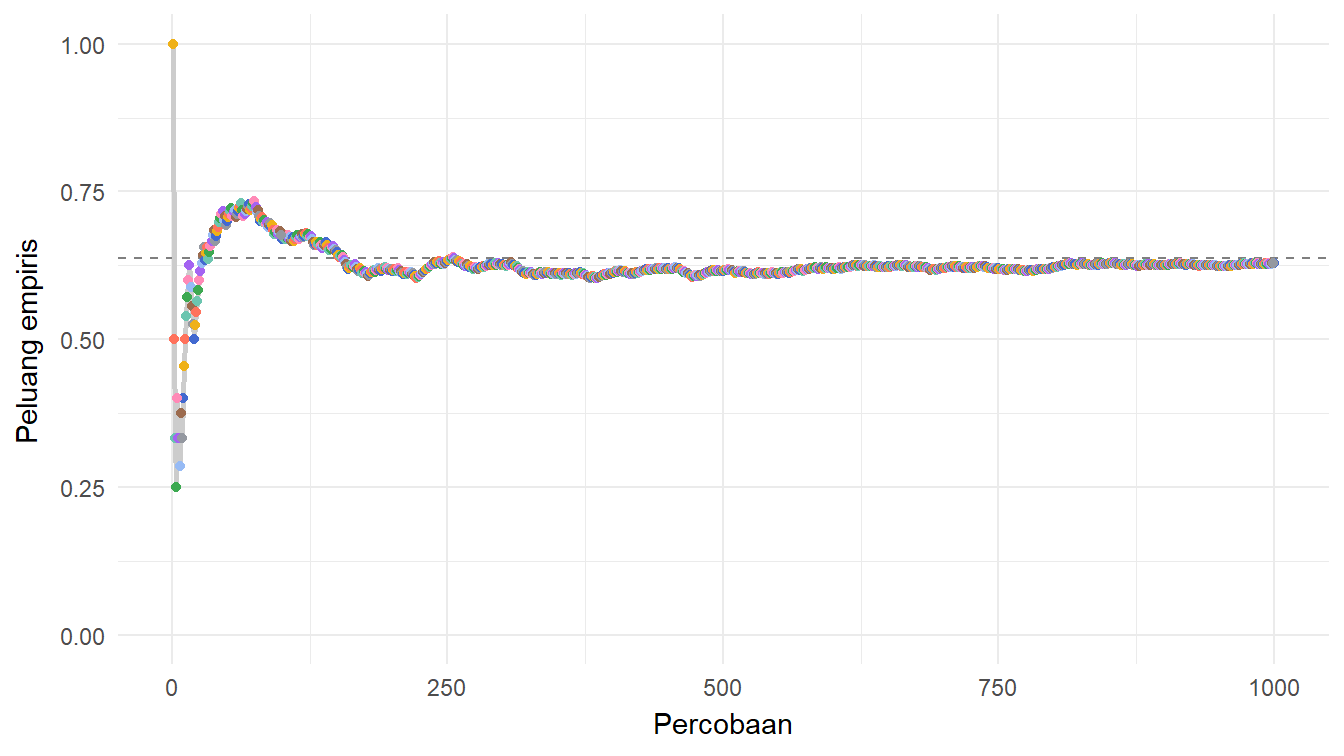
Kita telah membuat objek gganim plot_anim_p_empiris. Bagaimana animasi yang terbentuk? Perhatikan Gambar 10!

Kode 
plot_anim_p_empiris
Gambar 10: Ilustrasi perubahan peluang empiris dari satu percobaan ke percobaan berikutnya

Animasi Estimasi Nilai \(\pi\)

Gambar 10 menunjukkan bahwa semakin besar percobaannya, nilai peluang empirisnya semakin mendekati nilai peluang teoretisnya, yaitu \(\frac{2}{\pi}\). Jika \(P_{\text{empiris}}\) menotasikan nilai peluang empiris tersebut, kita mendapatkan Persamaan 3.

\[ P_{\text{empiris}} \approx \frac{2}{\pi} \tag{3}\]

Atau dengan kata lain, kita juga dapat menyatakan Persamaan 3 menjadi Persamaan 4.

\[ \pi \approx \frac{2}{P_{\text{empiris}}} \tag{4}\]

Nah, oleh karena itu kita dapat menggunakan nilai variabel dalam p_empiris dalam data_eksperimen untuk mendekati nilai \(\pi\). Kita lakukan hal ini dengan kode pada Daftar 15.

Daftar 15: Membuat estimasi nilai \(\pi\) dalam data_eksperimen
Kode 
data_eksperimen <- data_eksperimen |> 
  mutate(
    estimasi_pi = 2 / peluang_empiris
  )

Sekarang kita membuat animasi yang serupa dengan Gambar 10, tetapi yang akan kita plot adalah nilai-nilai variabel estimasi_pi. Kita melakukannya dengan kode pada Daftar 16.

Daftar 16: Membuat animasi estimasi nilai \(\pi\)
Kode 
plot_anim_mendekati_pi <- data_eksperimen |> 
  ggplot(aes(x = percobaan, y = estimasi_pi)) + 
  geom_hline(
    yintercept = pi,
    linetype = "dashed",
    color = "gray50"
  ) + 
  geom_line(
    color = "gray80",
    linewidth = 1
  ) + 
  geom_point(
    aes(color = warna, group = percobaan)
  ) + 
  scale_color_identity() + 
  theme_minimal() + 
  labs(
    x = "Percobaan",
    y = "Estimasi pi"
  ) + 
  transition_reveal(
    along = percobaan
  )

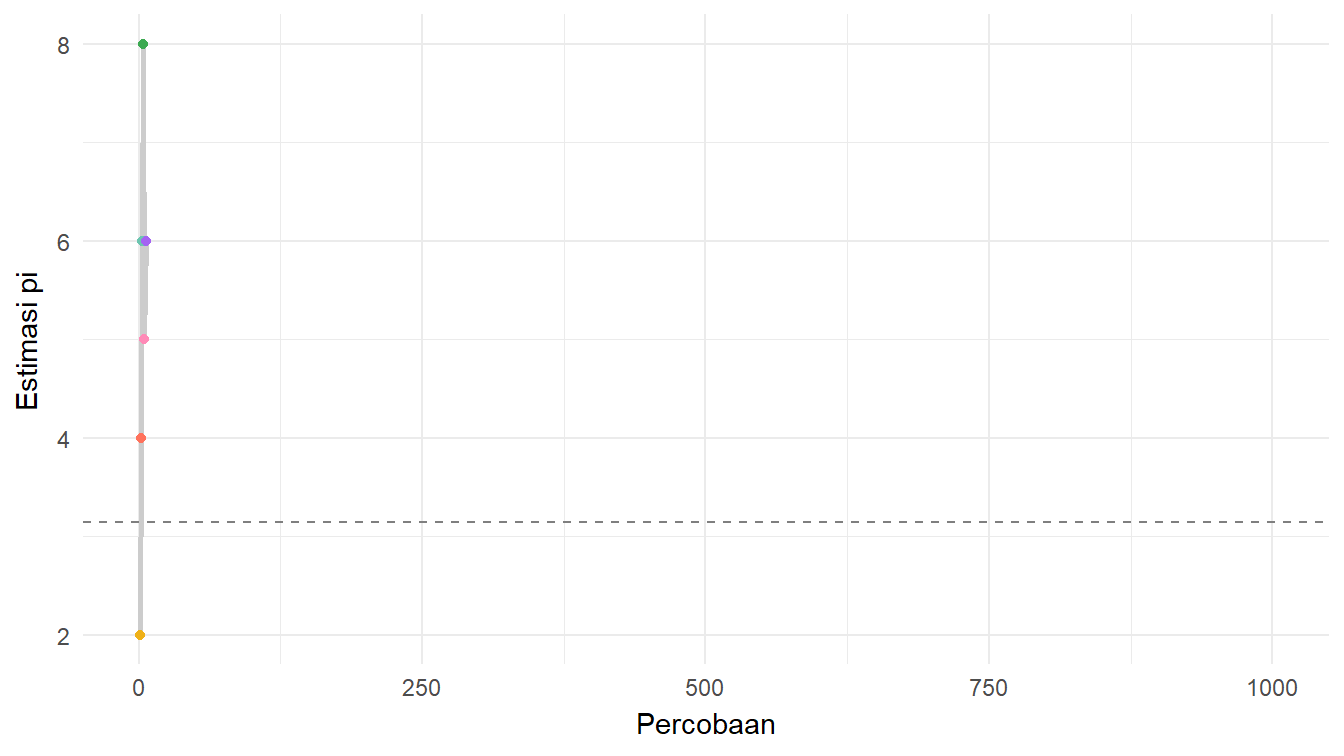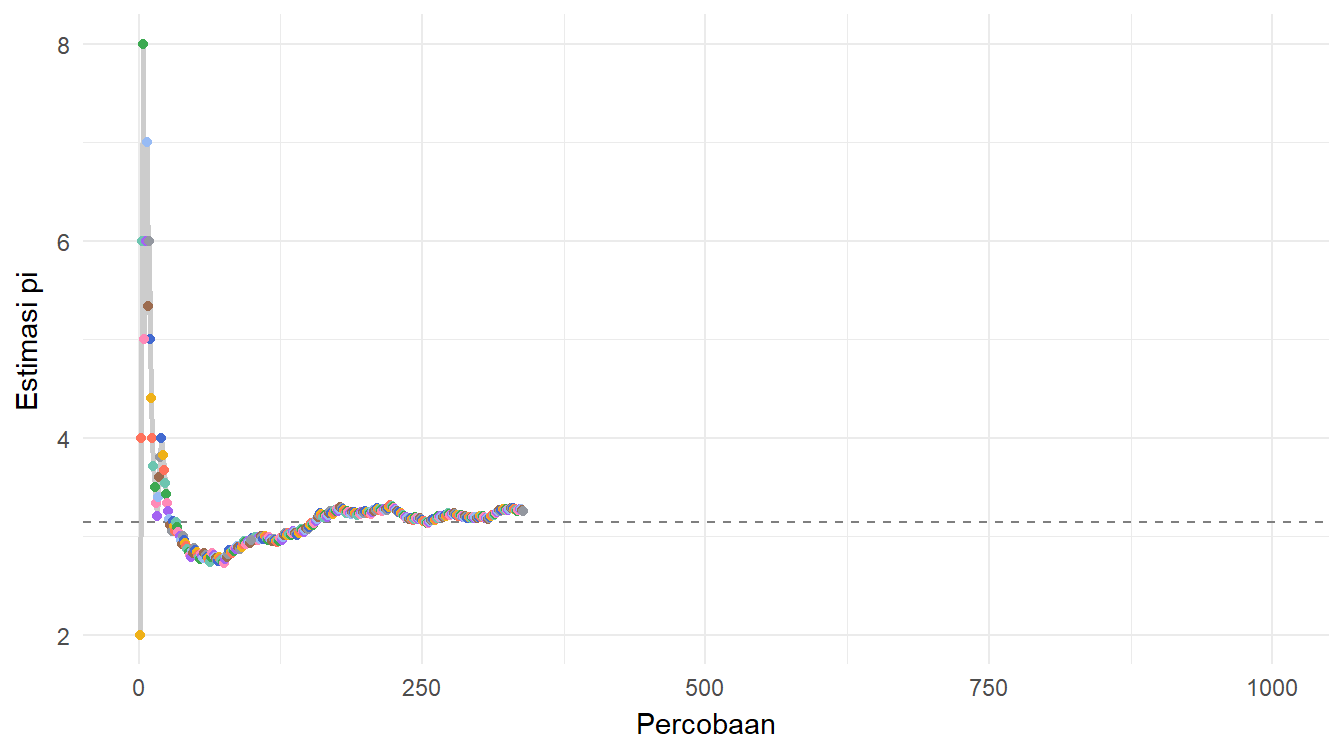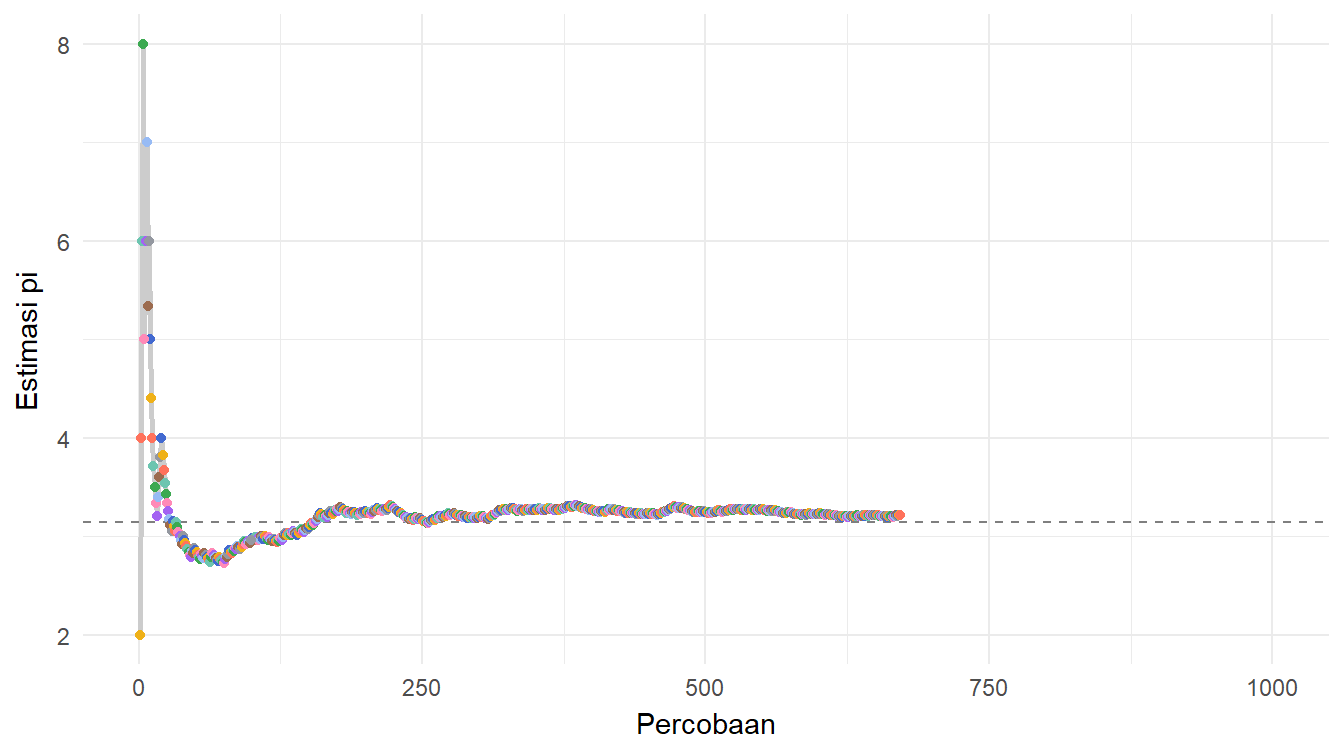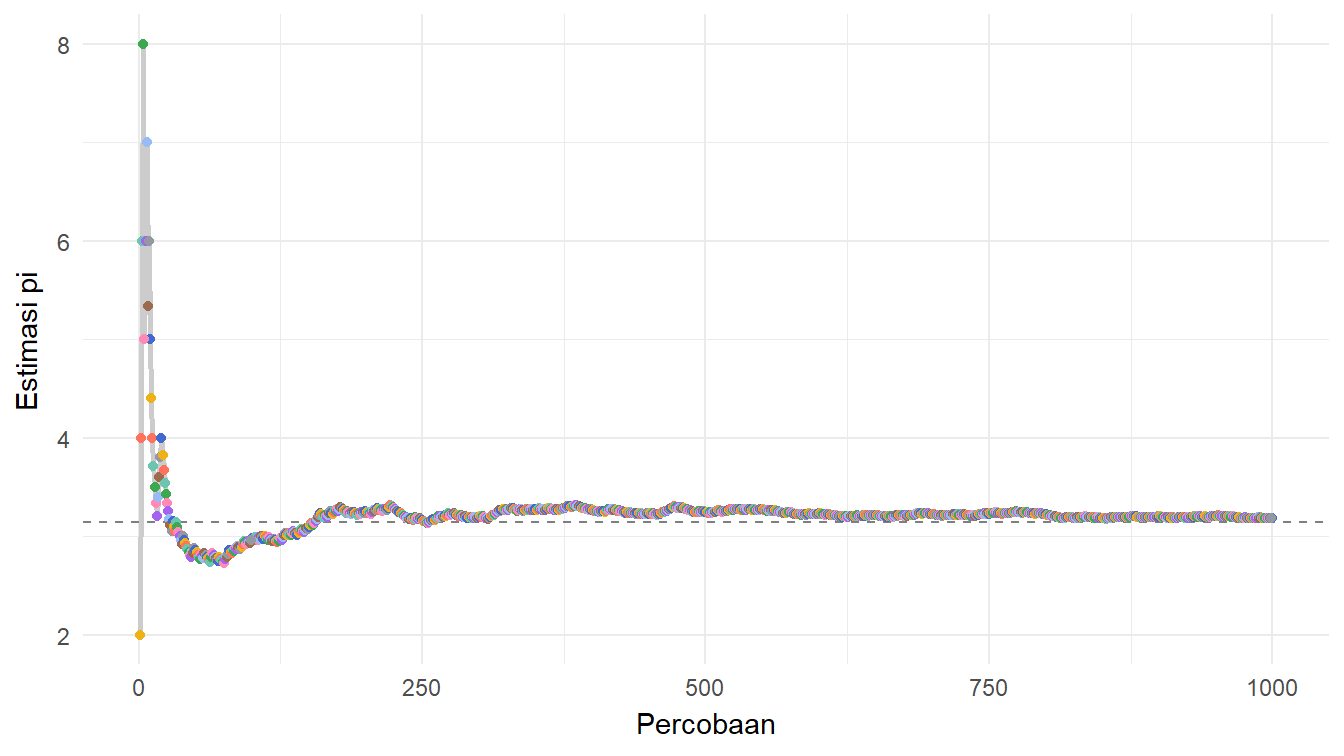
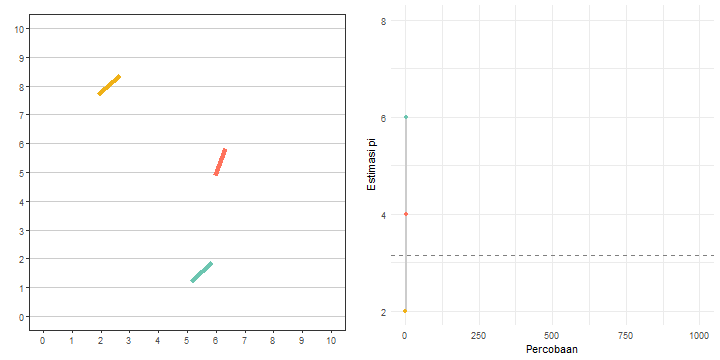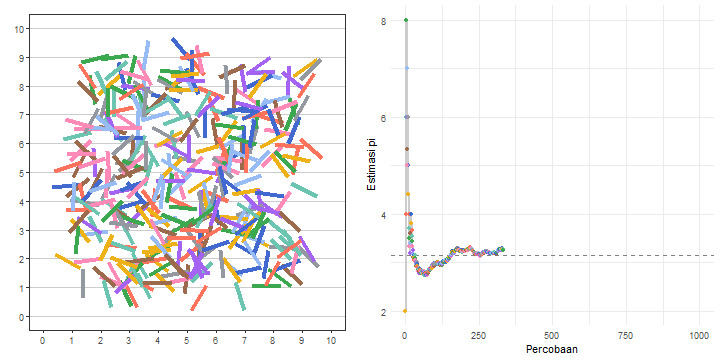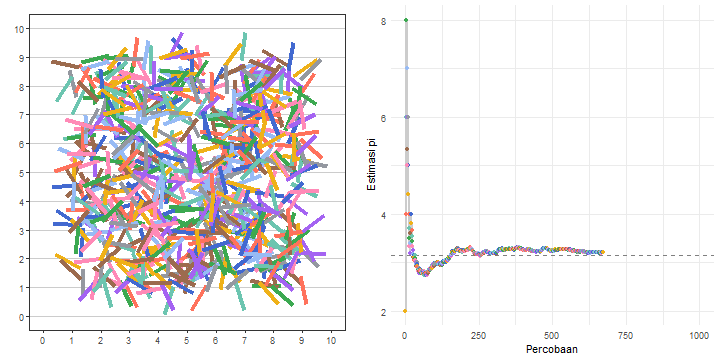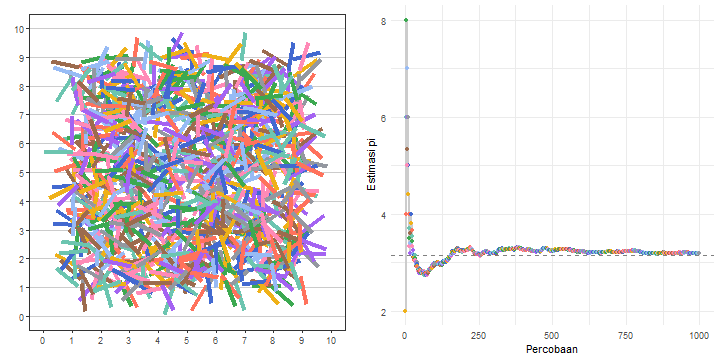
Gambar 11 mengilustrasikan bagaimana eksperimen jarum Buffon dapat digunakan untuk mengestimasi nilai \(\pi\).

Kode 
plot_anim_mendekati_pi
Gambar 11: Eksperimen jarum Buffon untuk mendekati nilai \(\pi\)

Berdasarkan hasil eksperimen jarum Buffon yang terdata dalam data_eksperimen, kita dapat melihat estimasi nilai \(\pi\)-nya pada percobaan yang terakhir, yaitu percobaan ke-1000. Berapa nilai estimasinya? Mari kita menggunakan Daftar 17 dan lihat luarannya.

Daftar 17: Menampilkan nilai estimasi_pi pada percobaan yang ke-1000
Kode 
est_pi <- data_eksperimen$estimasi_pi[1000]
est_pi
[1] 3.184713

Ternyata, kita mendapatkan nilai estimasinya sekitar 3,1847. Nilai estimasi ini tentu akan semakin dekat ke nilai \(\pi\) yang sebenarnya jika banyaknya percobaannya semakin besar.

Animasi Hasil Setiap Percobaan

Hasil setiap percobaan dalam eksperimen jarum Buffon juga dapat kita animasikan. Hal ini serupa dengan Gambar 8. Dengan cara yang serupa dengan pembuatan animasi-animasi sebelumnya, kita dapat melakukannya dengan kode pada Daftar 18.

Daftar 18: Membuat animasi hasil setiap percobaan
Kode 
plot_anim_hasil_percobaan <- data_eksperimen |> 
  ggplot(aes(x = theta_l, y = d_h)) +
  geom_line(
    data = data_kurva_sin,
    aes(x = x, y = y),
    color = "#efb118",
    linewidth = 1,
    inherit.aes = FALSE
  ) + 
  geom_point(
    aes(
      color = potong,
      group = percobaan
    ),
    size = 3
  ) +
  scale_color_manual(
    values = c(
      "Memotong" = "#4269d0",
      "Tak memotong" = "#ff725c"
    ),
    name = "Hasil percobaan"
  ) +
  theme_minimal() + 
  theme(
    legend.position = "bottom"
  ) + 
  labs(
    x = expression(theta[l]),
    y = expression(d[h])
  ) + 
  transition_reveal(
    along = percobaan
  )

Untuk melihat hasilnya, kita dapat mencetak objek gganim plot_anim_hasil_percobaan yang dihasilkan pada Daftar 18. Hasil animasinya disajikan pada Gambar 12.

Kode 
plot_anim_hasil_percobaan
Gambar 12: Animasi hasil setiap percobaan dalam eksperimen jarum Buffon

Gabungan Animasi

Seringkali gabungan animasi memberikan informasi yang lebih kaya daripada animasi tunggal. Misalnya, bagaimana menurutmu jika kita dapat mengatur agar animasi pada Gambar 9 dan Gambar 10 berdampingan? Selain kita dapat melihat eksperimen jarum Buffon, secara simultan kita juga dapat mengamati tren peluang empirisnya. Itulah yang akan kita lakukan. Untuk melakukannya, kita dapat menggunakan kode pada Daftar 19.

Daftar 19: Menyandingkan animasi eksperimen jarum Buffon dan peluang empirisnya 
# Membuat animasi eksperimen jarum Buffon
gif_anim_jarum <- animate(
  plot_anim_jarum,
  width = 360,
  height = 360,
  nframes = 200,
  fps = 10
)

# Membuat animasi tren peluang empiris
gif_anim_p_empiris <- animate(
  plot_anim_p_empiris,
  width = 360,
  height = 360,
  nframes = 200,
  fps = 10
)

# Membaca animasi sebagai kumpulan frame gambar
mgif_anim_jarum <- image_read(gif_anim_jarum)
mgif_anim_p_empiris <- image_read(gif_anim_p_empiris)

# Menggabungkan frame pertama dari kedua animasi secara berdampingan
gif_buffon_p_empiris <- image_append(
  c(mgif_anim_jarum[1], mgif_anim_p_empiris[1])
)

# Menggabungkan semua frame berikutnya satu per satu
for(i in 2:200){
  kombinasi <- image_append(
    c(mgif_anim_jarum[i], mgif_anim_p_empiris[i])
  )
  gif_buffon_p_empiris <- c(
    gif_buffon_p_empiris,
    kombinasi
  )
}

# Menyimpan hasil gabungan sebagai satu fail gif
anim_save(
  filename = "gif_buffon_p_empiris.gif",
  animation = gif_buffon_p_empiris
)

Kode pada Daftar 19 menghasilkan animasi yang berupa gambar gif. Animasi tersebut ditunjukkan pada Gambar 13.

Gambar 13: Ilustrasi eksperimen jarum Buffon dan peluang empirisnya

Dengan cara yang serupa, kita juga dapat menyandingkan animasi yang disajikan pada Gambar 9 dan Gambar 11. Animasi tersebut ditunjukkan pada Gambar 14.

Gambar 14: Ilustrasi eksperimen jarum Buffon untuk mendekati nilai pi

Kita juga dapat menyandingkan animasi yang disajikan pada Gambar 9 dan Gambar 12. Animasi tersebut ditunjukkan pada Gambar 15.

Gambar 15: Ilustrasi eksperimen jarum Buffon dan hasil setiap percobaannya

Catatan Akhir

Kita telah belajar banyak hal melalui masalah jarum Buffon. Pertama, kita telah mengetahui apa itu simulasi Monte Carlo pada Bagian 1. Simulasi itu kita gunakan untuk mengilustrasikan masalah jarum Buffon pada Bagian 2. Pada bagian itu kita memahami secara detail masalah jarum Buffon, khususnya pada Bagian 2.1. Pada Bagian 2.2 kita membuat “kanvas” untuk masalah tersebut, yaitu selembar kertas bergaris-garis. Pada Bagian 2.3 kita memvisualisasikan sebuah jarum. Selain itu, kita juga menemukan kondisi agar jarumnya memotong garis pada kertas. Pada Bagian 2.4 dan Bagian 2.5, kita melakukan eksperimen jarum Buffon dan memvisualisasikan hasilnya.

Tak hanya itu. Kita juga membuat visualisasi hasil eksperimen jarum Buffon menjadi lebih hidup dengan memanfaatkan animasi. Hal ini kita lakukan pada Bagian 3. Pada Bagian 3.5, kita menggabungkan animasi-animasi yang dihasilkan untuk menyampaikan pesan yang lebih efektif dan efisien. Misalnya, Gambar 13 menampilkan pesan yang kuat bahwa peluang empirisnya semakin mendekati ke nilai tertentu, yaitu \(\frac{2}{\pi}\), ketika percobaannya semakin banyak, sembari kita memantau apa yang terjadi dengan eksperimennya.

Artikel ini memiliki keterbatasan. Pertama adalah penggunaan asumsi bahwa panjang jarumnya adalah \(l = 1\) dan jarak antargaris pada kertasnya adalah \(d = 1\). Kamu dapat mengeksplorasi lebih lanjut bagaimana jika panjang jarumnya lebih panjang daripada jarak antargarisnya, ataupun sebaliknya. Selain itu, pembuatan jarum dalam artikel ini menggunakan koordinat satu titik ujung dan besar sudut kemiringannya, untuk menentukan koordinat titik ujung lainnya. Kamu dapat menggunakan cara lain. Misalnya, diketahui koordinat titik tengah jarum dan besar sudutnya, lalu gunakan informasi tersebut untuk menentukan kedua titik ujung jarumnya. Selamat mencoba!

Kembali ke atas

Penggunaan Kembali