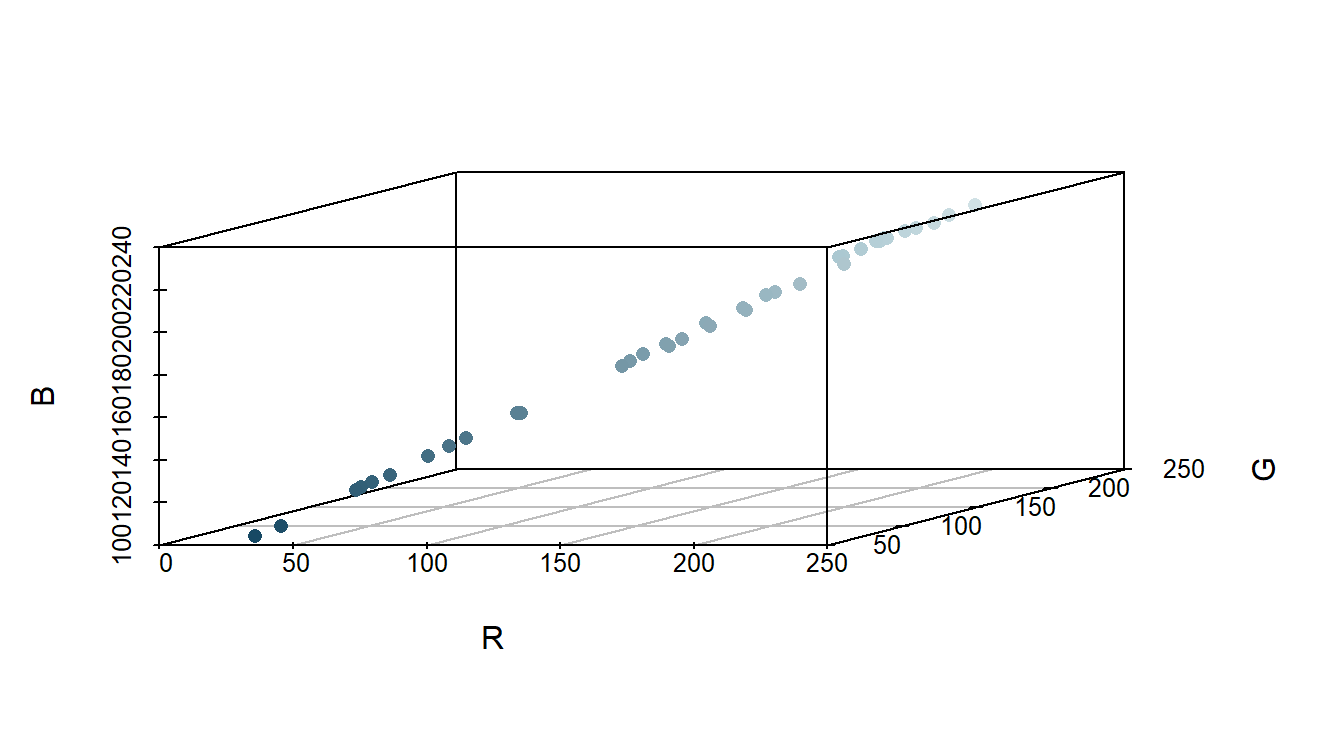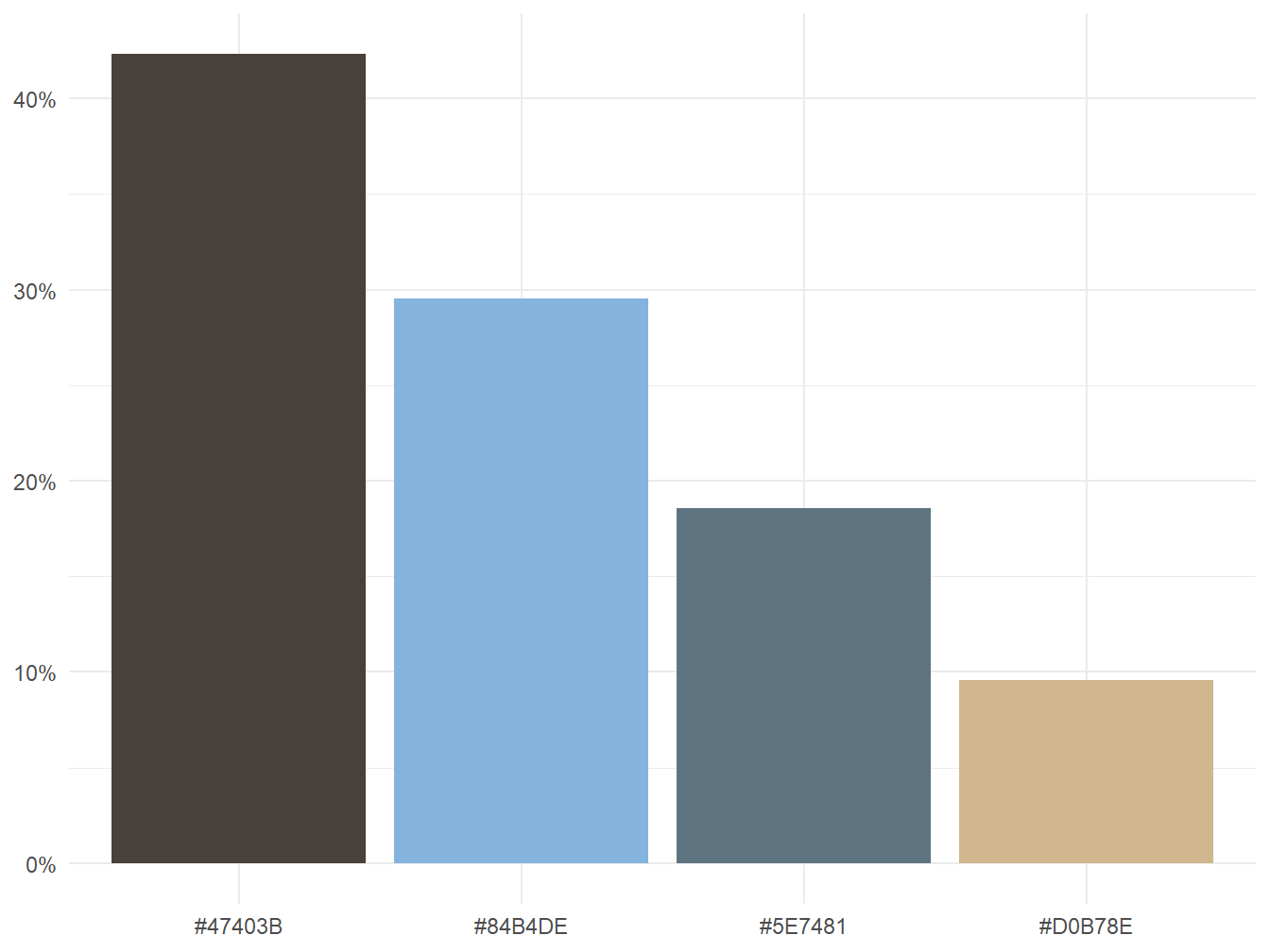Apa yang kamu lihat dari sebuah foto? Mungkin kamu melihat kenangan yang tersimpan. Mungkin kamu juga ingin menggali pesan yang tersirat. Oke, mari kita melihat sebuah foto atau gambar dari sudut pandang yang berbeda! Kita dapat melihat sebuah gambar sebagai matriks.
Perhatikan Gambar 1! Apa yang dilihat oleh orang dalam meme pada Gambar 1? Karena terlalu kecil, mari kita memperbesarnya dan menaruhnya ke bidang koordinat Kartesius. Kita lakukan hal itu dengan pemrograman R. Untuk itu, kita panggil paket-paket yang kita perlukan seperti pada Daftar 1.
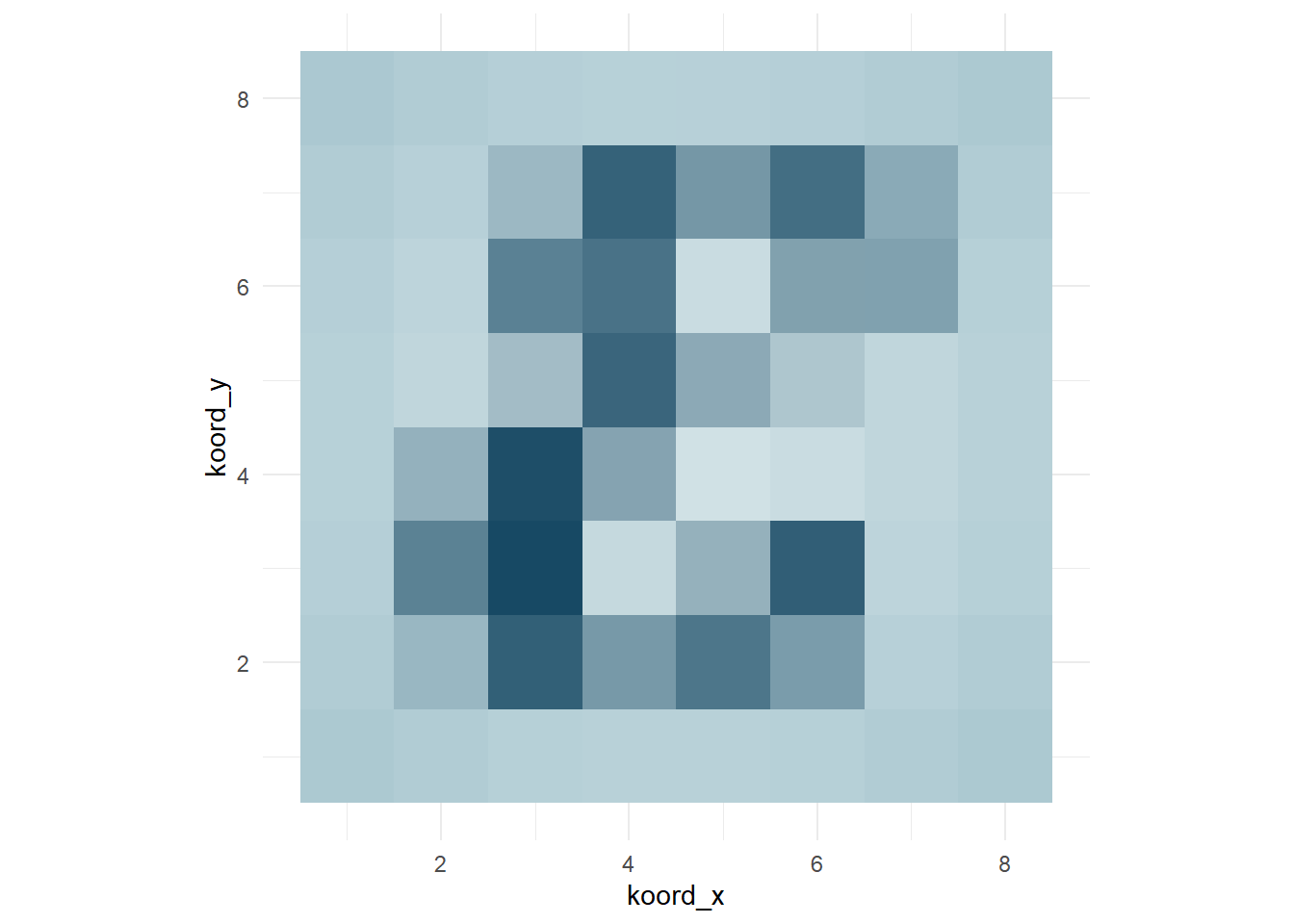
Paket-paketnya telah siap. Kita lanjut memperbesar gambar yang dilihat oleh orang dalam meme tersebut dan memposisikannya dalam bidang koordinat Kartesius. Perhatikan Gambar 2!
Sekarang, apa yang kamu amati dari Gambar 2? Ternyata itu adalah simbol epsilon. Meskipun tampak kabur, piksel-piksel epsilon tersebut tampak jelas. Setiap piksel berkorespondensi dengan satu warna. Warna tersebut dapat dinyatakan ke dalam tiga warna dasarnya, yaitu RGB (red, green, dan blue). Dengan demikian, kita dapat menyatakan gambar tersebut sebagai tiga matriks warna dasar: \(R\), \(G\), dan \(B\).
[1] "Matriks R" 1 2 3 4 5 6 7 8
[1,] 171 177 181 183 183 181 177 172
[2,] 177 183 156 53 117 67 138 177
[3,] 181 189 90 73 201 129 128 182
[4,] 183 192 163 58 140 174 192 184
[5,] 183 148 30 133 208 201 192 184
[6,] 181 91 23 197 149 49 189 182
[7,] 177 153 50 119 77 122 183 177
[8,] 172 177 182 184 184 182 177 172[1] "Matriks G" 1 2 3 4 5 6 7 8
[1,] 200 204 207 209 208 207 204 201
[2,] 204 208 184 98 151 110 170 204
[3,] 207 212 129 114 220 161 161 208
[4,] 209 214 188 101 169 198 214 209
[5,] 209 177 78 163 225 220 214 209
[6,] 207 130 73 217 177 94 212 208
[7,] 204 183 96 153 118 156 208 204
[8,] 201 204 208 209 209 208 204 201[1] "Matriks B" 1 2 3 4 5 6 7 8
[1,] 209 212 215 216 216 215 212 209
[2,] 212 216 195 121 166 131 183 212
[3,] 215 219 148 135 225 174 175 215
[4,] 216 220 198 124 182 206 220 216
[5,] 216 189 104 177 229 225 220 216
[6,] 215 148 100 222 188 118 219 215
[7,] 212 194 119 168 138 171 216 212
[8,] 209 212 215 216 216 215 212 209Okay, kita telah dapat melihat sebuah gambar dengan menggunakan matriks-matriks \(R\), \(G\), dan \(B\). Kita dapat memasangkan nilai-nilai yang bersesuaian dari matriks tersebut sebagai triplet. Misalnya, komponen pada baris pertama dan kolom pertama dalam matriks-matriks \(R\), \(G\), dan \(B\), secara berturut-turut adalah 171, 200, dan 209. Dengan demikian, kita mendapatkan satu triplet \(\left( 171,200,209 \right)\). Dengan cara ini, kita juga dapat membuat 63 triplet lainnya.
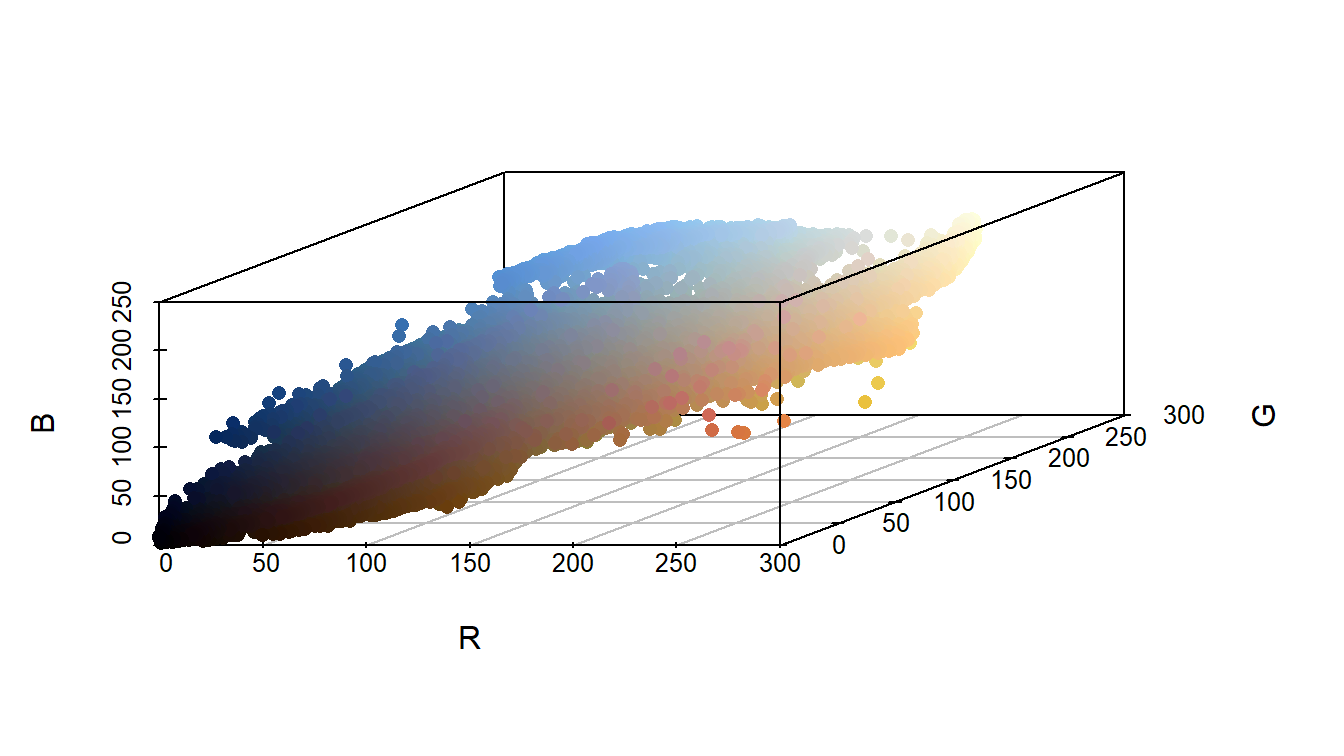
Sekarang kita memiliki 64 triplet. Semua triplet yang merepresentasikan warna tersebut dapat kita plot dalam ruang dimensi tiga. Hasilnya ditunjukkan pada Gambar 3.
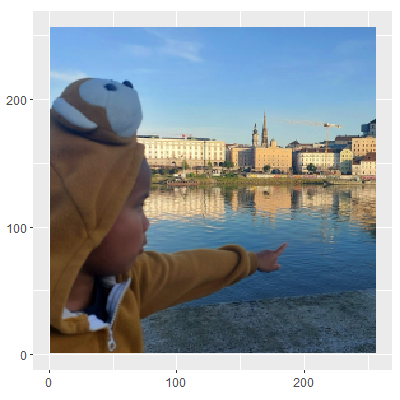
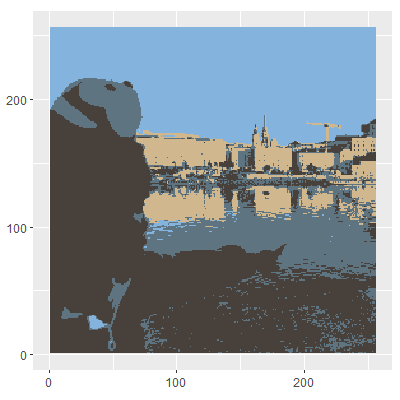
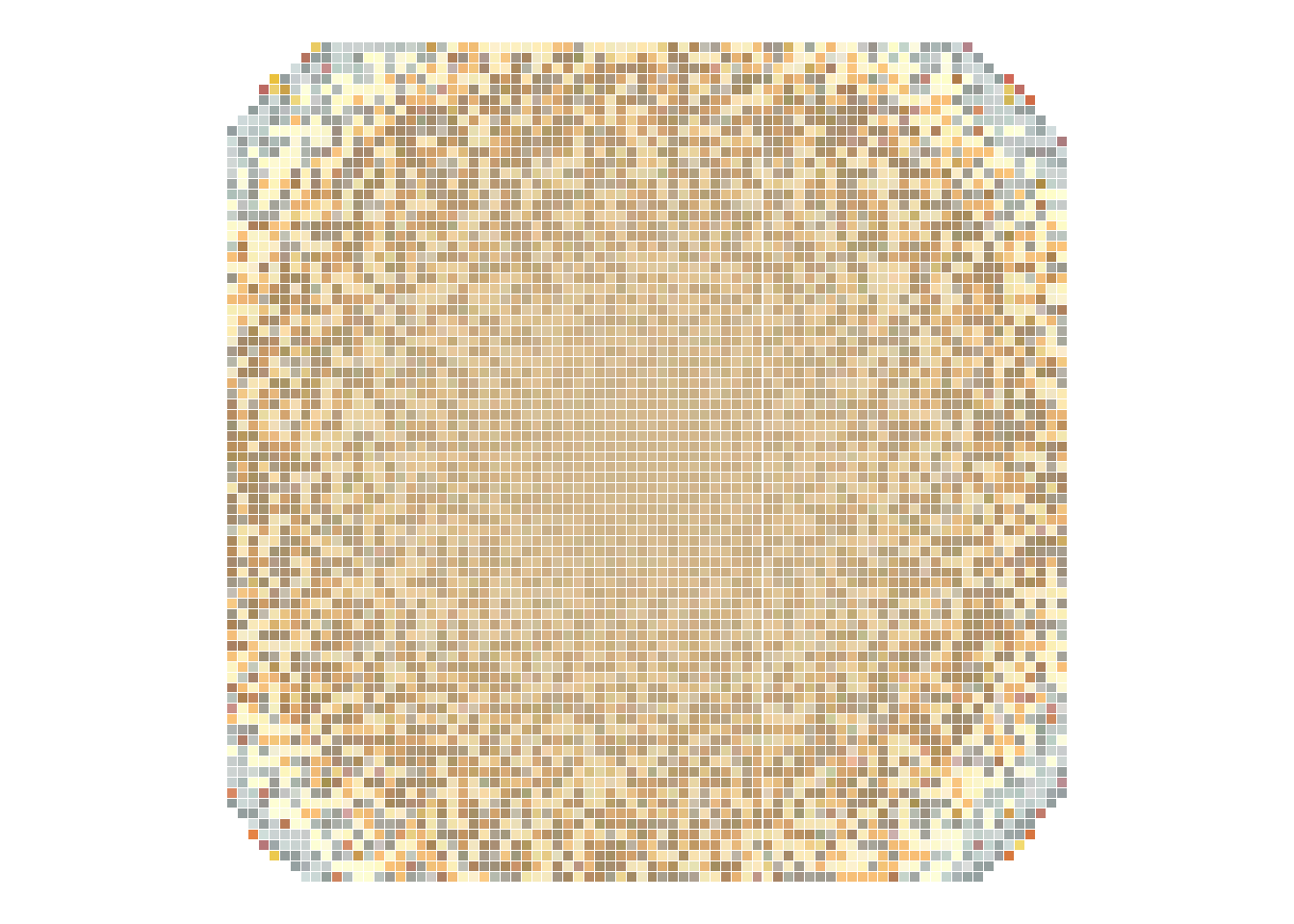
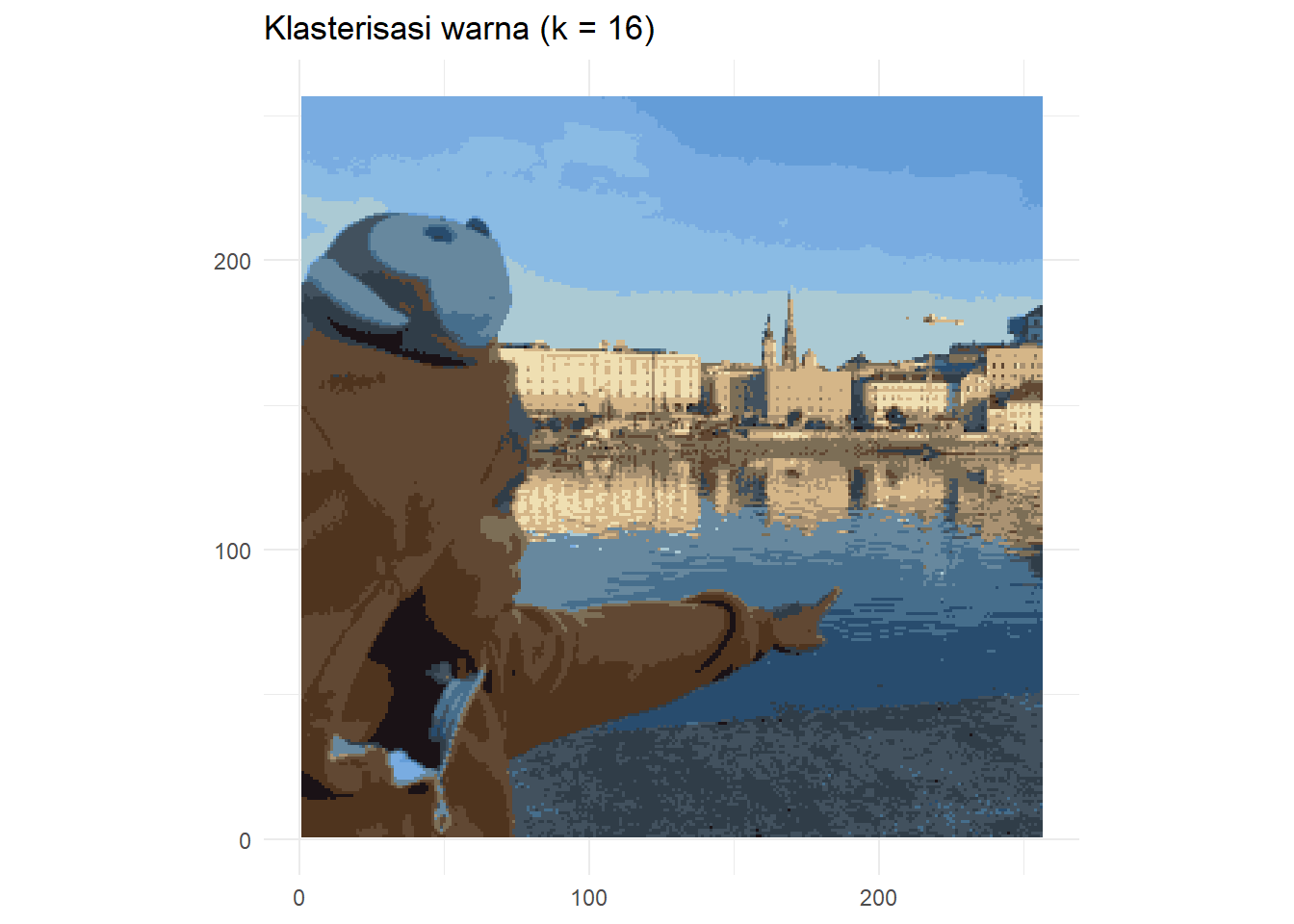
Nah, sekarang kita dapat melihat sebuah gambar atau foto dengan menggunakan matriks, yaitu tiga matriks warna dasarnya. Dari tiga matriks tersebut, kita dapat mengkonstruksi titik-titik yang merepresentasikan warna tersebut ke dalam ruang dimensi tiga. Kita gunakan perspektif seperti ini untuk memanipulasi sebuah foto sehingga variasi warnanya tereduksi. Tujuan kita berikutnya adalah untuk membuat foto Gambar 4 (a) menjadi Gambar 4 (b). Hal ini telah dijanjikan pada pos sebelumnya.
Bagaimana cara mencapai tujuan tersebut? Mari kita bahas gambaran umumnya terlebih dahulu pada bagian berikutnya.
Ide Dasar
Untuk menyerhanakan warna foto pada Gambar 4 (a), kita gunakan perspektif yang telah dibahas pada bagian sebelumnya. Setelah itu, kita terapkan klasterisasi \(k\)-rerata terhadap titik-titik warna yang dihasilkan. Secara umum, tahapan-tahapan utama yang nanti kita lakukan adalah sebagai berikut.
Mengekstrak data warna R, G, dan B dari foto.
Klasterisasi \(k\)-rerata terhadap data warna.
Mengganti setiap warna pada foto asli dengan pusat klasternya.
Dengan cara seperti itu, kita akan mendapatkan sebuah foto yang hanya memuat \(k\) warna. Warna-warna itu diperoleh dari pusat klaster-klaster yang terbentuk. Tak perlu berlama-lama, mari kita mulai tahapan pertamanya.
Mengekstrak Data Warna
Tahapan pertamanya adalah mengestrak data warna dari sebuah foto. Foto awal yang kita gunakan adalah foto pada Gambar 4 (a). Untuk melakukannya, kita gunakan kode pada Daftar 2.
Kode
# Memuat dan menskala gambar
foto_ku <- image_read(
"aset/karuna_donau.png"
) |>
image_scale("256x256!")
# Ekstrak data mentah piksel
data_mentah_foto <- image_data(foto_ku)
# Ukuran foto
lebar_foto <- dim(data_mentah_foto)[2]
tinggi_foto <- dim(data_mentah_foto)[3]
# Konversi ke data frame dan membalik koordinat y
rgb_foto_df <- as.data.frame.table(data_mentah_foto, responseName = "nilai") |>
mutate(
kanal = as.integer(Var1),
koord_x = as.integer(Var2),
koord_y = as.integer(Var3),
nilai = as.integer(nilai)
) |>
select(kanal, koord_x, koord_y, nilai) |>
pivot_wider(
names_from = kanal,
values_from = nilai,
names_prefix = "ch"
) |>
transmute(
koord_x,
koord_y = tinggi_foto - koord_y + 1,
R = ch1,
G = ch2,
B = ch3,
R_norm = R / 255,
G_norm = G / 255,
B_norm = B / 255,
warna_hex = rgb(R_norm, G_norm, B_norm)
)
head(rgb_foto_df)# A tibble: 6 × 9
koord_x koord_y R G B R_norm G_norm B_norm warna_hex
<int> <dbl> <int> <int> <int> <dbl> <dbl> <dbl> <chr>
1 1 256 117 171 233 0.459 0.671 0.914 #75ABE9
2 2 256 117 173 234 0.459 0.678 0.918 #75ADEA
3 3 256 116 172 233 0.455 0.675 0.914 #74ACE9
4 4 256 116 172 233 0.455 0.675 0.914 #74ACE9
5 5 256 115 170 234 0.451 0.667 0.918 #73AAEA
6 6 256 120 171 234 0.471 0.671 0.918 #78ABEA Dari kode di atas, kita mendapatkan data warna rgb_foto_df. Data tersebut memuat koordinat piksel-pikselnya (koord_x dan koord_y), warna dasar setiap pikselnya (R, G, dan B), dan warna-warna dasar tersebut yang telah diskala agar minimumnya 0 dan maksimumnya 1 (R_norm, G_norm, dan B_norm). Selain itu, kita juga membuat kolom warna_hex untuk merangkum informasi warna pada kolom-kolom R, G, dan B.
Mari kita selami rgb_foto_df lebih mendalam. Untuk itu, kita gambarkan diagram pencar untuk variabel-variabel warnanya, yaitu R, G, dan B. Perhatikan Gambar 5!
Klasterisasi \(K\)-Rerata
Selanjutnya, kita lakukan klasterisasi terhadap rgb_foto_df dengan menggunakan variabel-variabel R_norm, G_norm, dan B_norm. Untuk melakukannya, kita menggunakan fungsi kmeans(). Fungsi ini menggunakan input sebuah matriks. Oleh karena itu, terlebih dahulu kita membuat matriks tersebut. Matriks tersebut memuat tiga kolom, yaitu R_norm, G_norm, dan B_norm. Perhatikan Daftar 3!
Kita telah memperoleh matriks_foto. Kita siap untuk melakukan klasterisasi \(k\)-rerata dengan fungsi kmeans(). Perhatikan Daftar 4.
Hasil klasterisasi tersebut kita simpan sebagai sebuah objek dengan nama hasil_krerata. Terdapat informasi penting yang terkandung dalam hasil_krerata, yaitu cluster (klaster) dan centers (pusat setiap klaster). Kedua informasi tersebut berguna untuk mengidentifikasi klaster-klaster warnanya dan menyederhanakan warna-warnanya dengan pusat klasternya.
Sekarang, kita membuat rgb_foto_klaster_df yang memuat informasi klaster dan pusatnya tersebut dalam kolom-kolom klaster dan pusat_hex. Perhatikan Daftar 5. Untuk melihat beberapa baris awalnya, kita terapkan head() pada data tersebut.
Kode
rgb_foto_klaster_df <- rgb_foto_df |>
mutate(
klaster = hasil_krerata$cluster,
pusat_R = hasil_krerata$centers[klaster, "R_norm"],
pusat_G = hasil_krerata$centers[klaster, "G_norm"],
pusat_B = hasil_krerata$centers[klaster, "B_norm"]
) |>
mutate(
pusat_hex = rgb(pusat_R, pusat_G, pusat_B)
) |>
select(koord_x, koord_y, R, G, B, warna_hex, klaster, pusat_hex)
head(rgb_foto_klaster_df)# A tibble: 6 × 8
koord_x koord_y R G B warna_hex klaster pusat_hex
<int> <dbl> <int> <int> <int> <chr> <int> <chr>
1 1 256 117 171 233 #75ABE9 3 #84B4DE
2 2 256 117 173 234 #75ADEA 3 #84B4DE
3 3 256 116 172 233 #74ACE9 3 #84B4DE
4 4 256 116 172 233 #74ACE9 3 #84B4DE
5 5 256 115 170 234 #73AAEA 3 #84B4DE
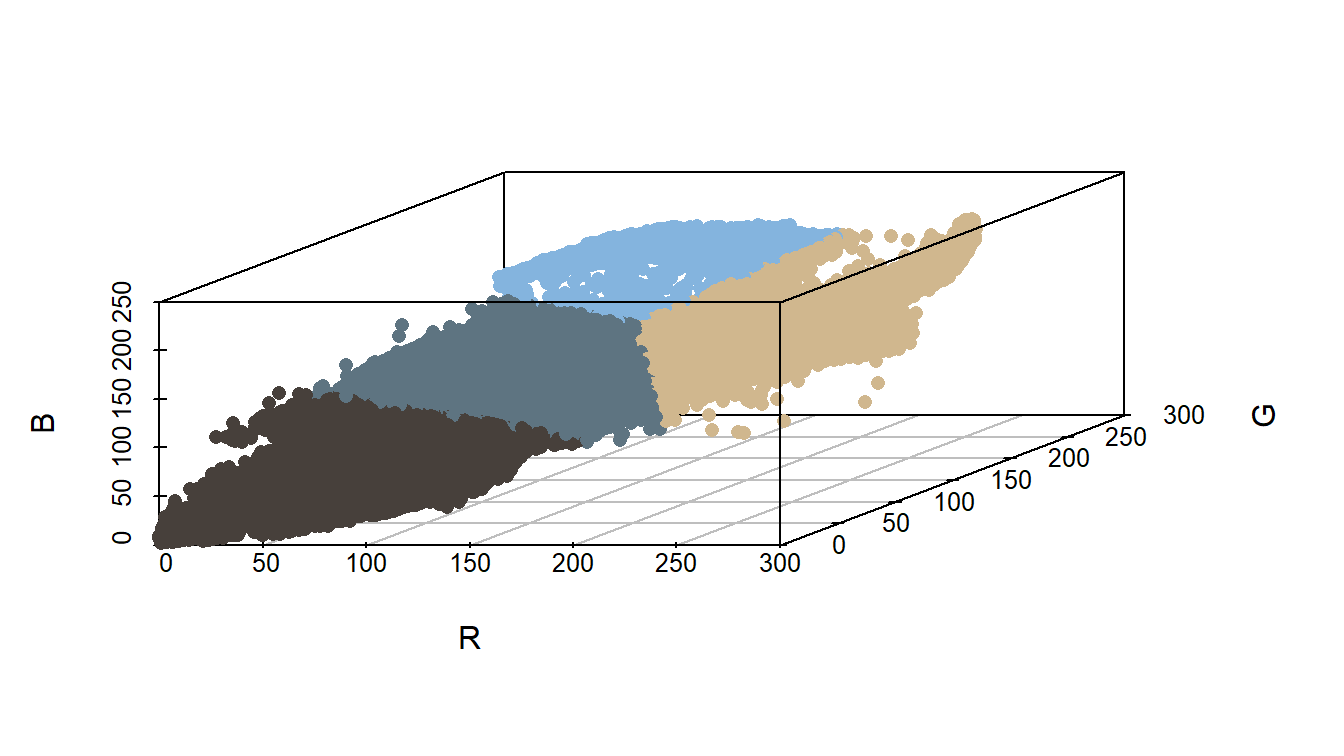
6 6 256 120 171 234 #78ABEA 3 #84B4DE Dari data yang telah kita buat di atas, kita dapat memvisualisasikan warna-warna yang masuk ke dalam setiap klasternya. Perhatikan Gambar 6!
Menyederhanakan Warna
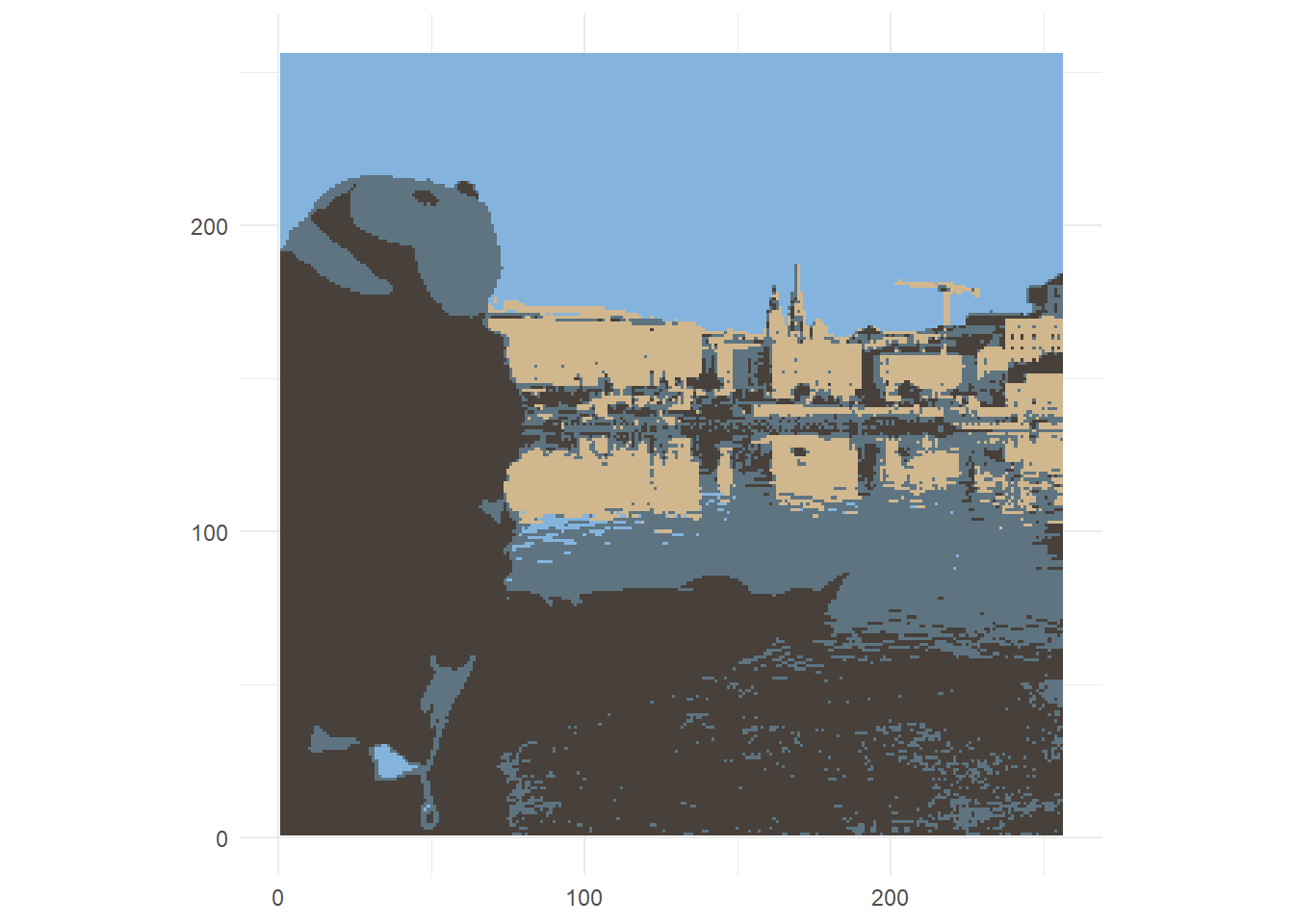
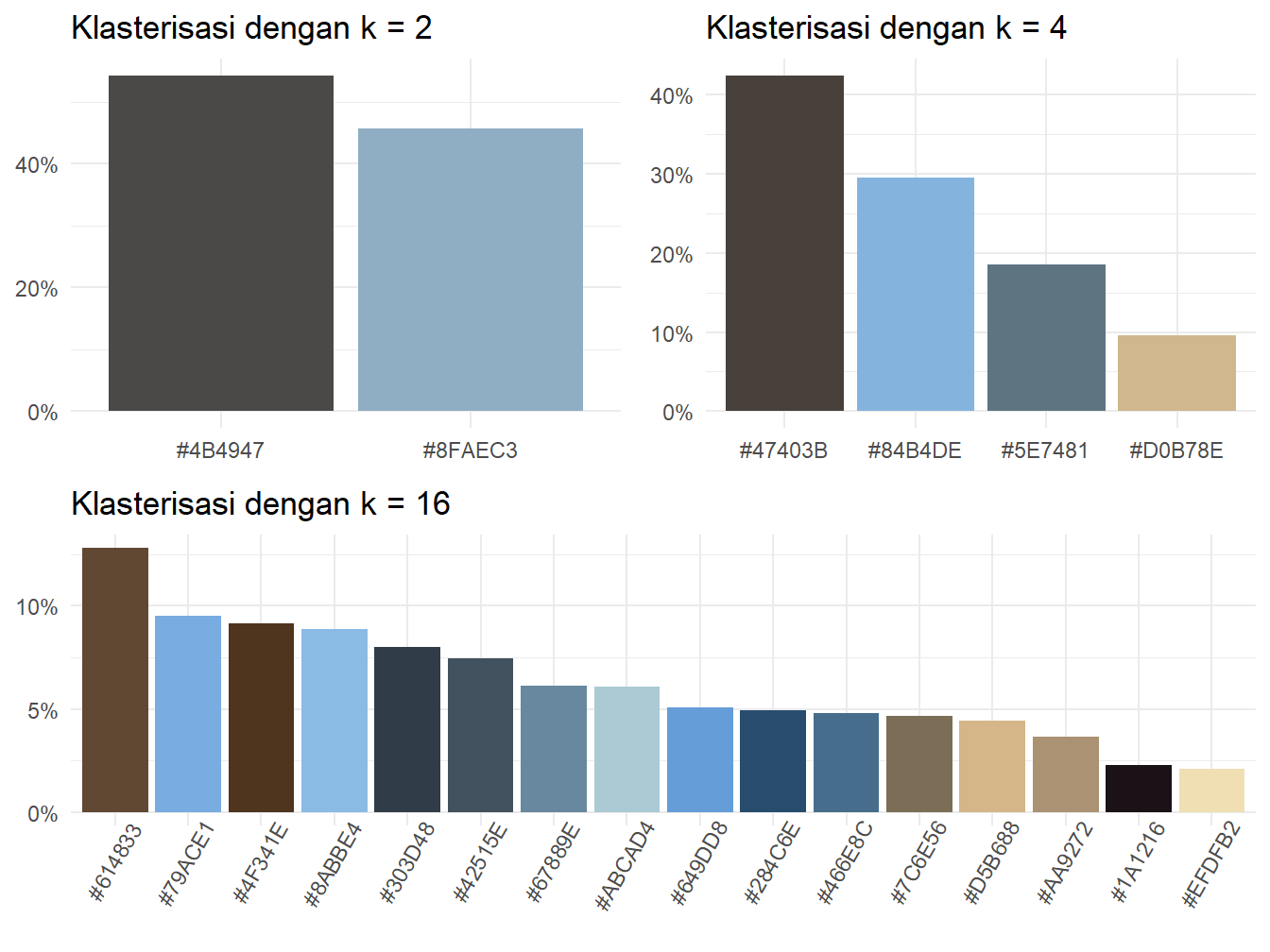
Tiba saatnya kita menyederhanakan warna. Caranya adalah dengan mengganti setiap warna dengan pusat klasternya. Mari kita lihat kembali rgb_foto_klaster_df. Data ini hanya memuat \(k=4\) warna, seperti yang ditunjukkan pada luaran Daftar 6 berikut.
# A tibble: 4 × 2
pusat_hex n
<chr> <int>
1 #47403B 27742
2 #5E7481 12175
3 #84B4DE 19353
4 #D0B78E 6266Kita dapat melihat kembali titik-titik warnanya ke dalam ruang dimensi tiga agar dapat mengamati hasil klasterisasi warnanya. Perhatikan Gambar 7!
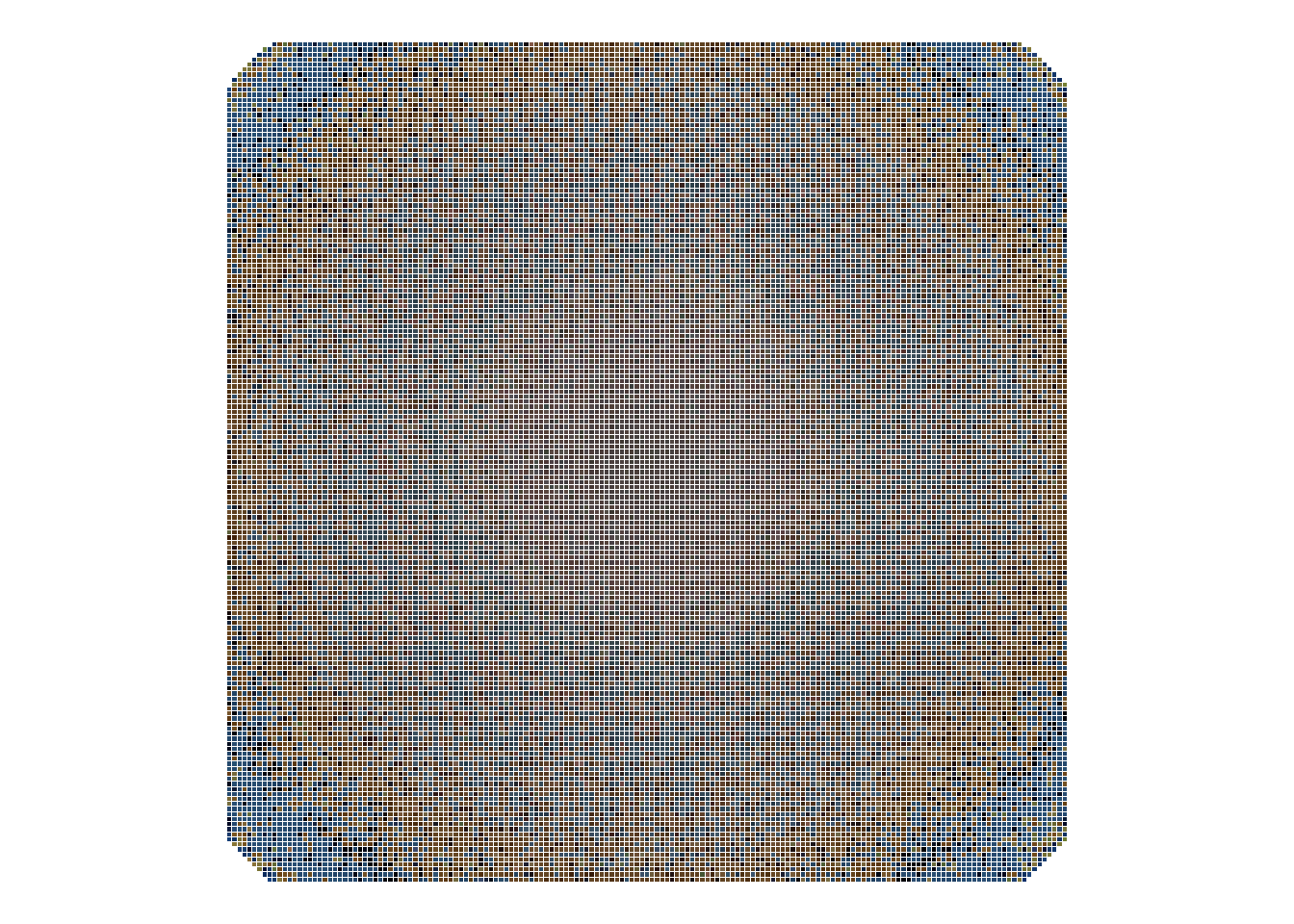
Sekarang, kita gambarkan kembali piksel-piksel dalam rgb_foto_klaster_df pada bidang koordinat Kartesius dengan kode pada Daftar 7. Hasilnya ditunjukkan pada Gambar 8.
Kode
rgb_foto_klaster_df |>
ggplot(
aes(x = koord_x, y = koord_y, fill = pusat_hex)
) +
geom_tile() +
scale_fill_identity() +
coord_equal() +
theme_minimal() +
theme(
axis.title = element_blank()
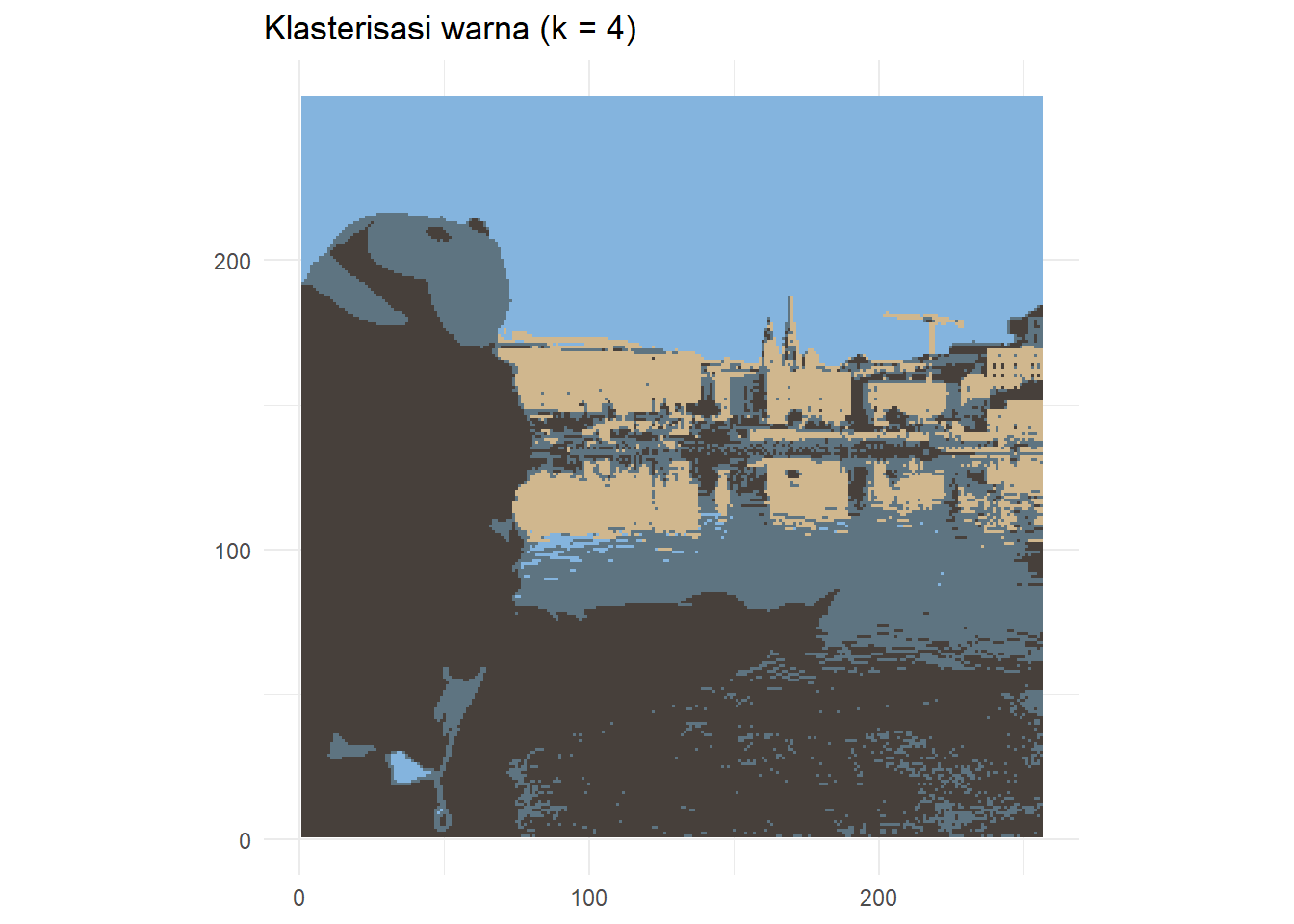
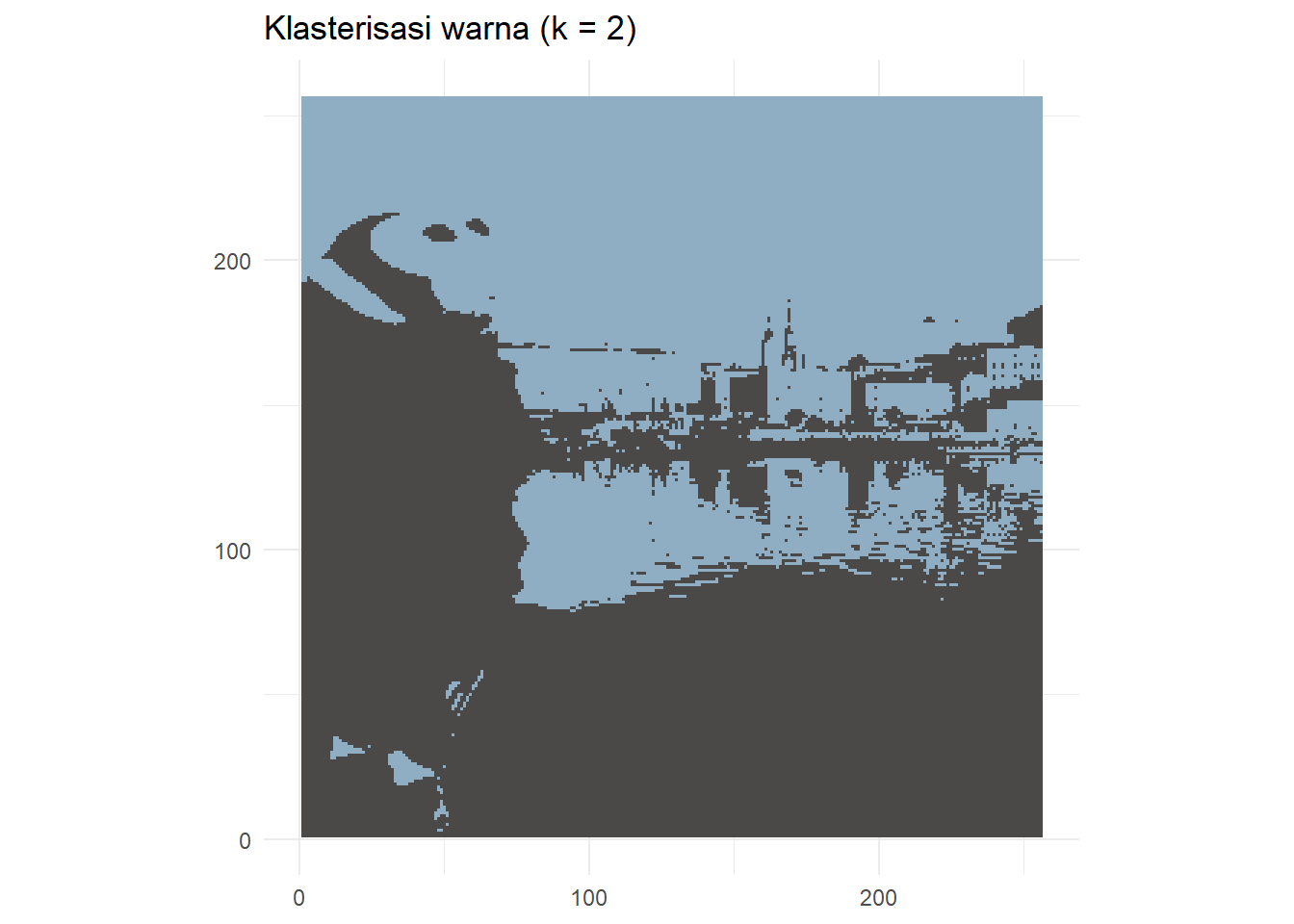
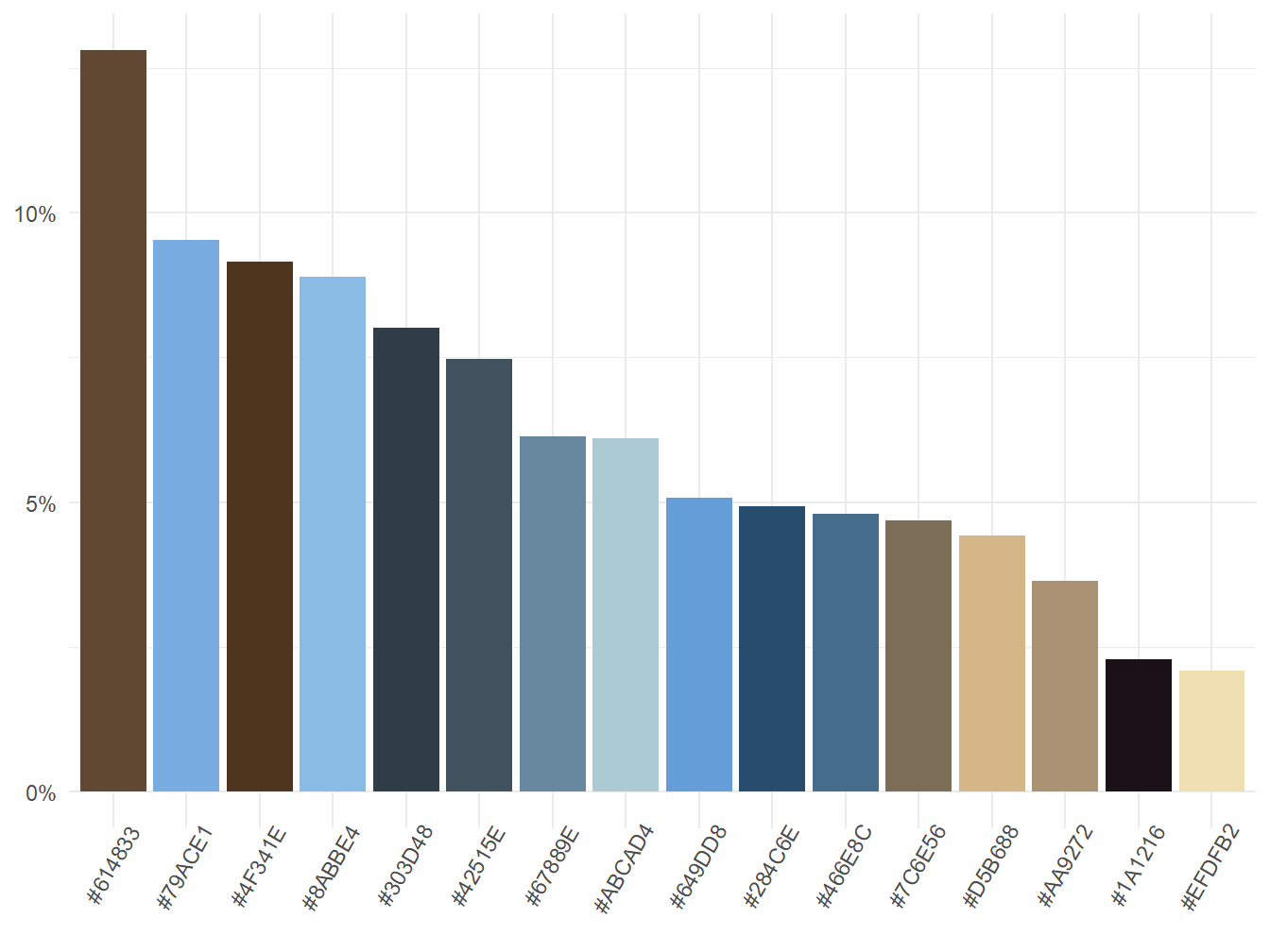
)Sampai di sini kita telah berhasil mereduksi variasi warna dari sebuah foto. Teknik yang telah kita lakukan tersebut tentu juga dapat diterapkan dengan \(k\) yang berbeda. Misalnya, kita juga dapat melakukannya dengan \(k\) = 16 dan 2. Hasilnya disajikan pada Gambar 9.
Mungkin kamu penasaran bagaimana komposisi warna dalam foto yang variasi warnanya sudah berkurang tersebut. Mari kita selidiki dan hasilnya disajikan pada Gambar 10.
Catatan Akhir
Kita telah mereduksi variasi warna dalam sebuah foto dengan menggunakan klasterisasi \(k\)-rerata. Untuk melakukannya, kita perlu mengetahui bagaimana sebuah foto atau gambar dapat direpresentasikan dengan matriks-matriks warna dasarnya. Setelah itu, kita ekstrak data warna piksel-piksel dalam gambar tersebut. Hal ini kita lakukan pada Bagian 2. Setelah kita mendapatkan data warna tersebut, kita gunakan data tersebut untuk melakukan klasterisasi \(k\)-rerata (lihat Bagian 3). Di akhir, kita ubah warna tiap-tiap pikselnya dengan warna pusat klasternya. Dengan cara ini, kita mendapatkan gambar yang hanya tersusun dari \(k\) warna. Hasil akhirnya dapat dilihat pada Gambar 9.
Sebagai catatan, kita menggunakan klasterisasi \(k\)-rerata terhadap titik-titik warna yang dinyatakan ke dalam RGB. Algoritma \(k\)-rerata tersebut mengandalkan jarak untuk membuat klaster-klaster. Akan tetapi, persepsi kita terhadap warna tidaklah linear di RGB. Dalam RGB, dua warna mungkin memiliki jarak yang dekat, tetapi secara intuitif kita menilai warna tersebut jauh berbeda. Sebaliknya, mungkin ada dua warna yang jauh secara numerik dalam ruang RGB, tetapi bagi kita dua warna itu dekat secara intuitif. Oleh karena itu, kita dapat memilih format warna yang lebih sesuai dengan persepsi kita, misalnya Lab. Silakan gunakan metode yang kamu pelajari di artikel ini, tetapi dengan menggunakan ruang warna Lab.