Klasterisasi K-Rerata

Langkah Demi Langkah Klasterisasi dengan Pemrograman R

Mulai dari memanipulasi gambar sampai menghindari paradoks Simpson, itulah manfaat analisis klaster. Artikel ini membahas secara tuntas analisis klaster yang sederhana, yaitu klasterisasi k-rerata (k-means clustering), mulai dari menjelaskan algoritmanya seperti apa sampai mendemonstrasikan algoritma tersebut secara mendetail.
klasterisasi
tutorial
visualisasi data
Pengarang
Afiliasi

Yosep Dwi Kristanto

Pendidikan Matematika, Universitas Sanata Dharma, Yogyakarta

Terbit

September 23, 2025

Kata kunci

analisis klaster, klasterisasi, k-rerata, k-means clustering, machine learning, ilmu data, paradoks Simpson, pemelajaran mesin, pemelajaran statistik, statistical learning

Ada banyak metode untuk memanipulasi sebuah gambar. Salah satunya ditunjukkan pada Gambar 1. Apa perbedaan gambar sebelah kiri dan kanan pada gambar tersebut?

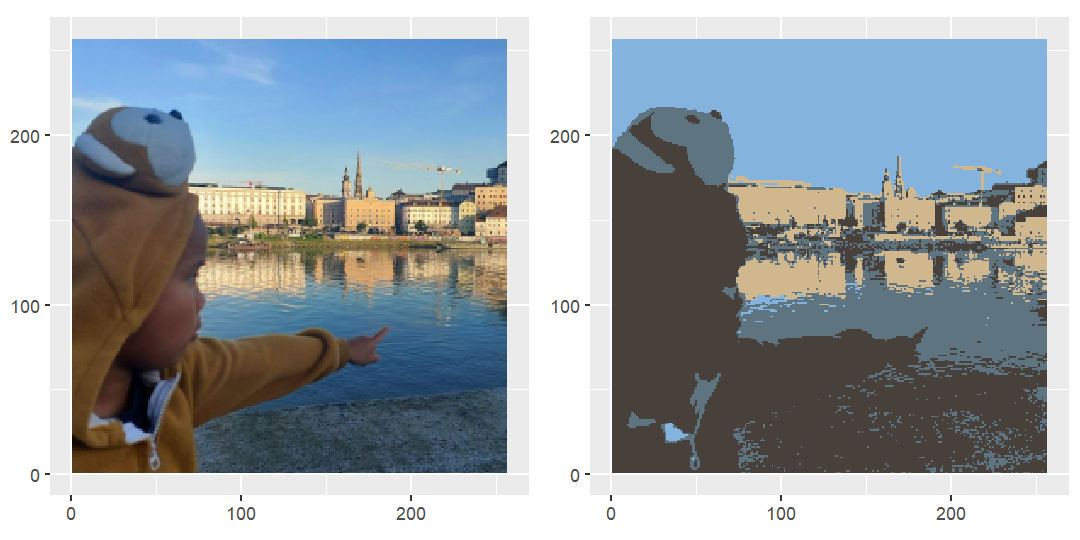
Gambar 1: Gambar asli (kiri) dan gambar setelah dimanipulasi (kanan)

Yup! Gambar sebelah kiri memiliki warna yang lebih bervariasi daripada yang kanan. Faktanya, gambar di sebelah kiri memiliki hampir 40 ribu warna sedangkan yang sebelah kanan hanya empat warna saja. Bagaimana cara melakukannya?

Tentu ada banyak cara untuk melakukannya. Akan tetapi, salah satunya adalah dengan menggunakan klasterisasi \(k\)-rerata. Untuk itu, kita akan belajar teknik klasterisasi tersebut. Kita awali dengan (a) latar belakang perlunya klasterisasi, kemudian (b) kita belajar bagaimana algoritmanya bekerja, dan akhirnya (c) kita aplikasikan algoritma tersebut untuk membagi data menjadi beberapa klaster. Jangan khawatir, penerapan algoritmanya nanti kita lakukan secara langkah demi langkah. Kita lakukan semuanya dengan menggunakan pemrograman R. Untuk itu, kita buka paket-paket yang diperlukan.

Kode

Paradoks Simpson

Bayangkan kamu ingin menemukan model untuk datamu, misalnya contoh_data. Biasanya, kamu perlu memvisualisasikan data tersebut untuk melihat polanya. Diagram pencar data tersebut disajikan pada Gambar 2.

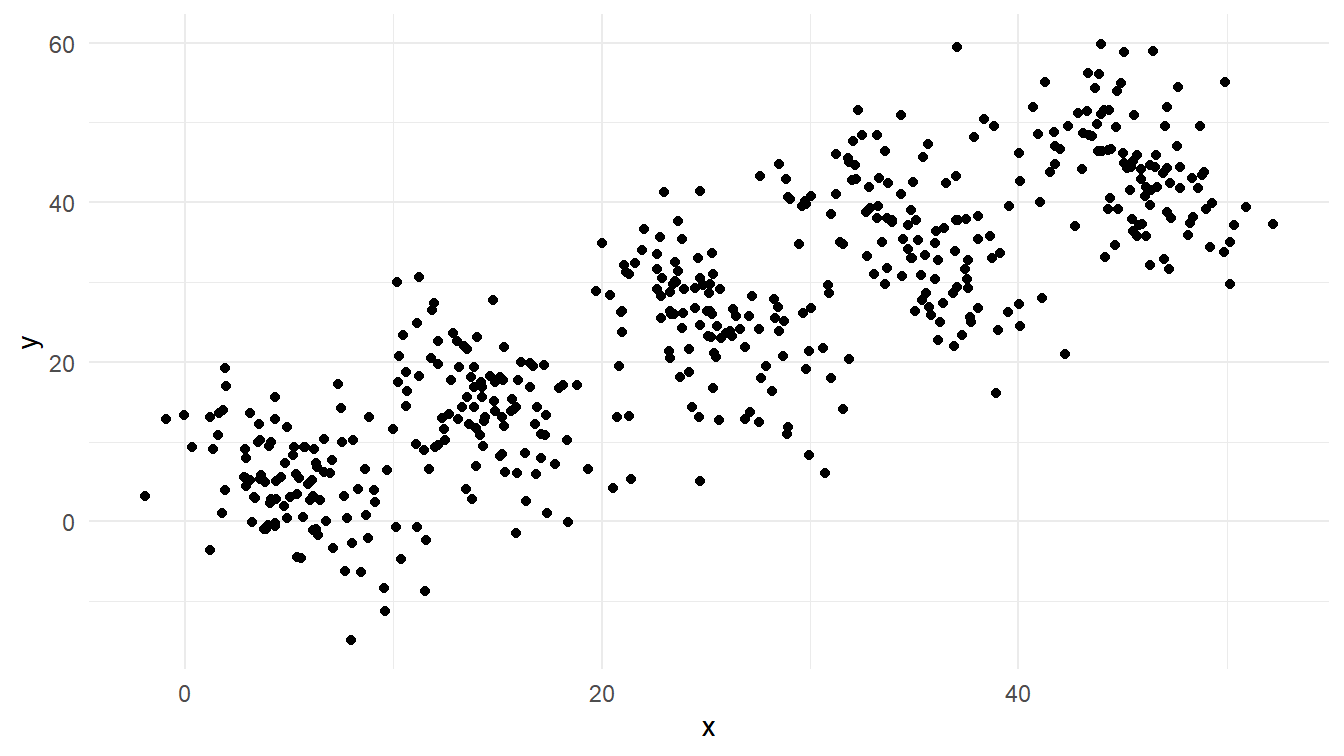
Gambar 2: Diagram pencar contoh_data

Berdasarkan Gambar 2, kamu kemungkinan besar menduga bahwa hubungan antara x dan y dalam data tersebut mengikuti model linear dengan korelasi positif: semakin besar nilai x, semakin besar juga nilai y. Dengan demikian, kamu akan mendapatkan model seperti yang ditunjukkan pada Gambar 3.

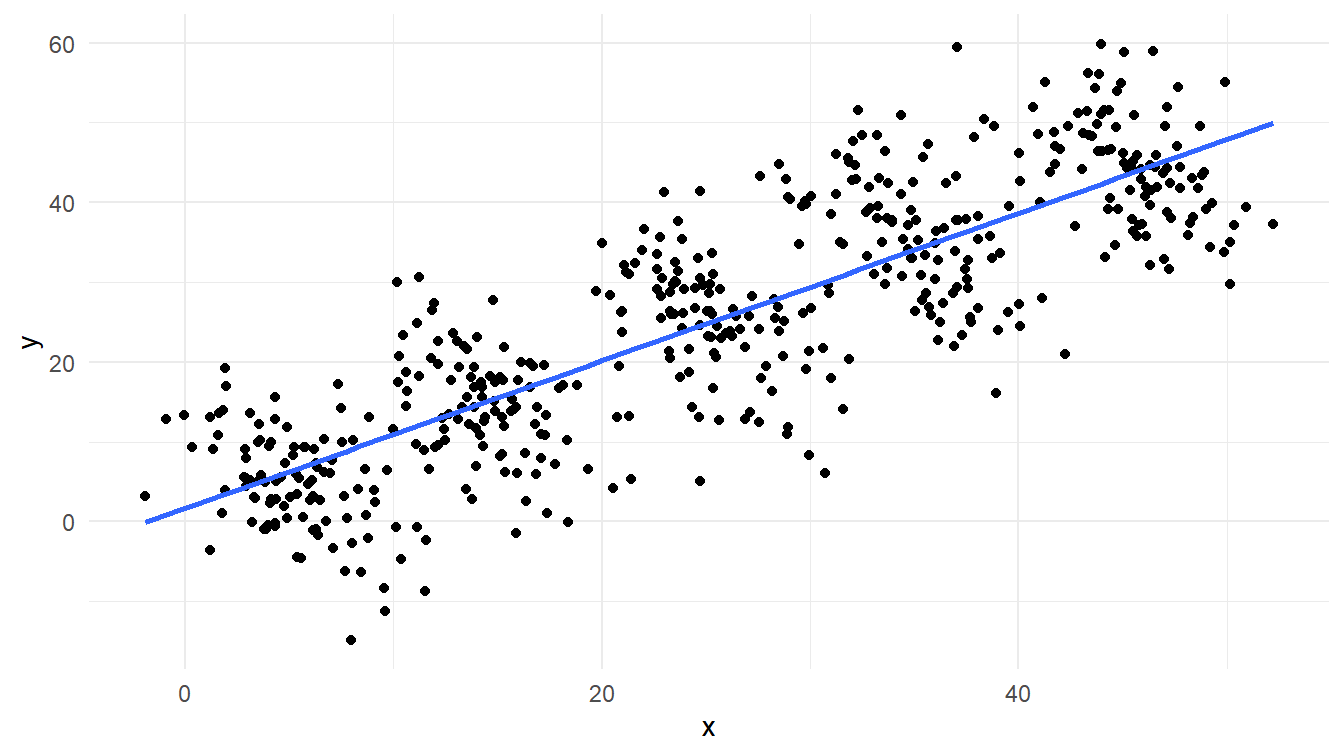
Gambar 3: Model linear untuk variabel-variabel x dan y dalam contoh_data

Akan tetapi, setelah dicermati kembali, tampaknya contoh_data tersebut terbagi menjadi beberapa klaster. Berdasarkan pengamatan terhadap Gambar 3 saja, kita dapat melihat bahwa data tersebut memiliki lima klaster. Setelah mempertimbangkan klaster-klaster tersebut, kita mendapatkan model linear yang sama sekali berbeda. Perhatikan Gambar 4!

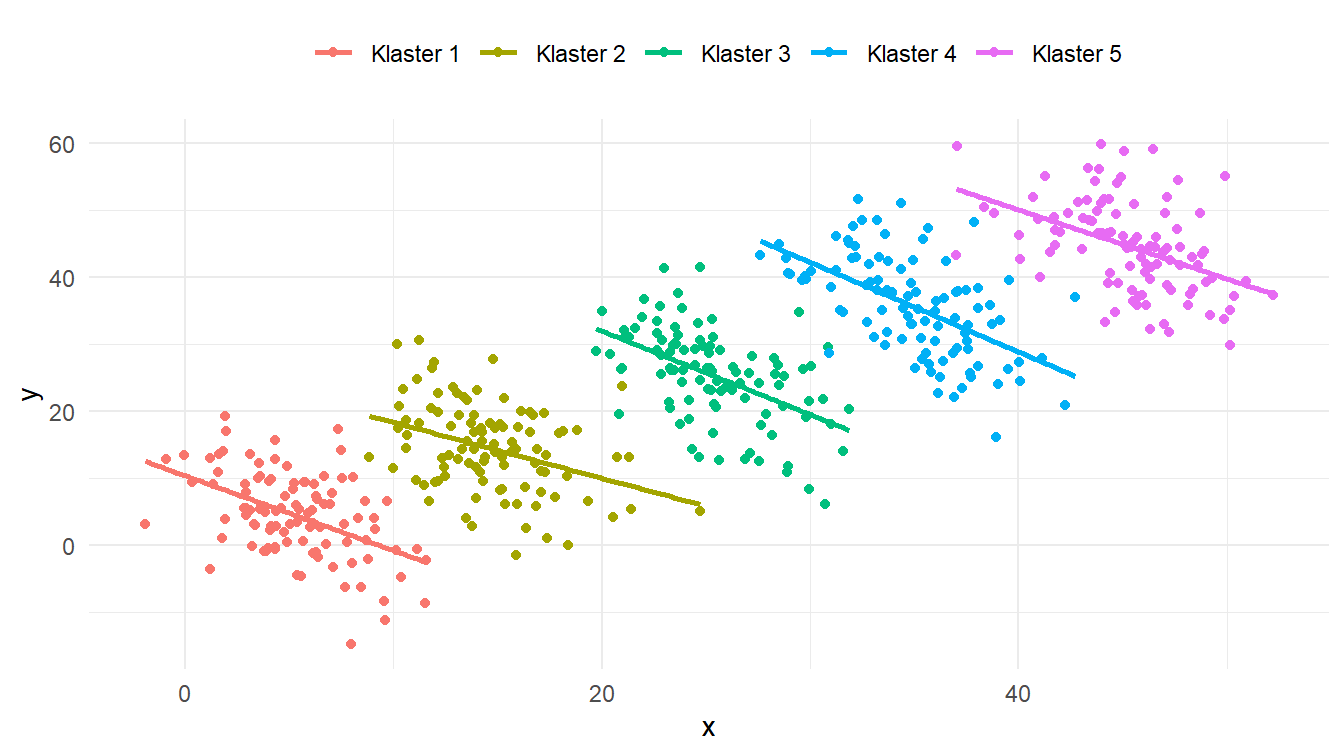
Gambar 4: Model linear untuk variabel-variabel x dan y setelah mempertimbangkan klaster-klaster dalam contoh_data

Fenomena yang baru saja kita alami tersebut dinamakan paradoks Simpson. Kita mendapatkan korelasi yang positif ketika kita tidak mempertimbangkan klaster, dan korelasinya negatif ketika kita mempertimbangkan klaster. Oleh karena itu, penting bagi kita untuk mencermati data secara lebih hati-hati, khususnya jika dalam data tersebut memuat beberapa klaster.

Informasi tentang klaster-klaster tersebut mungkin sudah ada dalam data. Akan tetapi, informasi tersebut juga mungkin belum ada. Jika klaster-klaster tersebut belum ada, kita dapat melakukan analisis klaster dengan menggunakan klasterisasi \(k\)-rerata (atau \(k\)-means clustering). Bagaimana caranya? Mari kita bahas di bagian berikutnya, Bagian 2.

Klasterisasi \(K\)-Rerata

Klasterisasi \(k\)-rerata merupakan algoritma pemelajaran mesin (machine learning) tanpa pengawasan yang membagi data tak berlabel menjadi \(k\) klaster yang berbeda dan tak saling tumpang tindih. Sebelum dilakukan klasterisasi ini, banyaknya klaster \(k\) perlu ditentukan terlebih dahulu. Algoritma klasterisasi ini adalah sebagai berikut.

  1. Inisialisasi: Pertama, kita pilih banyaknya klaster, yaitu \(k\). Setelah itu, algoritmanya akan memposisikan \(k\) titik secara acak sebagai pusat klaster (centroid) yang pertama.

  2. Penugasan: Setiap titik data dipasangkan ke pusat klaster terdekat. Proses ini menghasilkan \(k\) klaster awal.

  3. Pembaruan: Setelah semua titik masuk ke dalam klaster, algoritmanya kemudian menghitung kembali koordinat tiap-tiap pusat klasternya. Pusat klaster tersebut merupakan rerata dari semua titik dalam klaster tersebut.

  4. Ulangi: Langkah 2 dan 3 diulangi kembali. Ketika pusat klaster berpindah, setiap titik datanya dipasangkan kembali dengan pusat klaster baru yang terdekat, kemudian pusat setiap klasternya dihitung kembali. Proses ini diulang secara terus menerus sampai pusat klasternya tidak berpindah secara signifikan atau banyak maksimum iterasinya tercapai.

Penasaran dengan bagaimana algoritma tersebut bekerja? Pada bagian berikutnya, Bagian 3, kita akan menerapkan algoritma tersebut kepada Old Faithful Geyser.

Penerapan Algoritma \(K\)-Rerata

Kita terapkan algoritma \(k\)-rerata kepada data Old Faithful Geyser. Data ini sudah ada dalam R dengan nama faithful. Data ini memuat 272 baris dan dua variabel. Variabel waiting merupakan selang waktu antara dimulainya dua erupsi yang berurutan, sedangkan variabel eruptions merupakan lamanya erupsi yang kedua. Mari kita panggil data ini lihat beberapa barisnya dengan kode berikut.

Kode
data("faithful")

head(faithful)
  eruptions waiting
1     3.600      79
2     1.800      54
3     3.333      74
4     2.283      62
5     4.533      85
6     2.883      55

Kita dapat mengenal data faithful tersebut secara lebih dekat dengan membuat diagram pencarnya. Perhatikan Gambar 5!

Kode
faithful |> 
  ggplot(aes(x = eruptions, y = waiting)) + 
  geom_point() + 
  theme_minimal()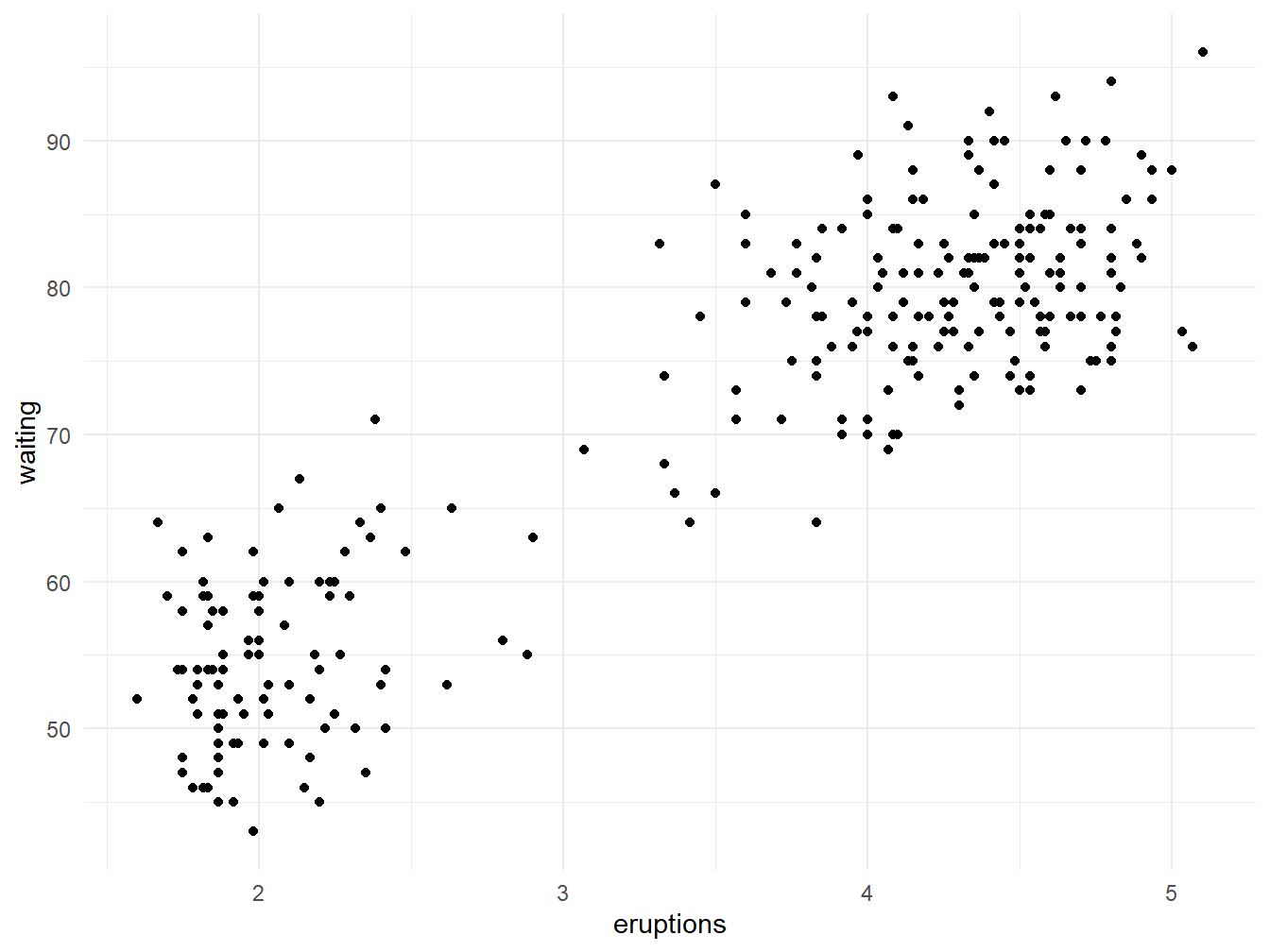
Gambar 5: Diagram pencar hubungan antara eruptions dan waiting dalam data faithful

Berdasarkan Gambar 5, kita dapat melihat bahwa tampaknya data faithful memiliki dua klaster. Oleh karena itu, kita akan pilih \(k=2\). Sebelum kita menerapkan algoritma \(k\)-rerata, terlebih dahulu kita normalbakukan variabel-variabel dalam data faithful tersebut. Mengapa demikian?

Klasterisasi \(k\)-rerata menggunakan jarak untuk menentukan klaster tiap-tiap titik datanya. Jika variabel-variabelnya memiliki skala yang berbeda (variabel eruptions merentang dari 1.6 sampai 5.1 sedangkan waiting merentang dari 43 sampai 96), variabel yang jangkauannya lebih besar tentu memiliki dampak besar terhadap perhitungan jaraknya. Hal ini akan menyebabkan hasil klasterisasinya tidak akurat.

Oleh karena itu, kita normalbakukan variabel-variabel eruptions dan waiting untuk membuat variabel-variabel baru, yaitu eruptions_std dan waiting_std. Untuk melihat hasilnya, kita dapat tampilkan beberapa baris pertamanya.

Kode
faithful <- faithful |> 
  mutate(
    eruptions_std = scale(eruptions),
    waiting_std = scale(waiting)
  )

head(faithful)
  eruptions waiting eruptions_std waiting_std
1     3.600      79    0.09831763   0.5960248
2     1.800      54   -1.47873278  -1.2428901
3     3.333      74   -0.13561152   0.2282418
4     2.283      62   -1.05555759  -0.6544374
5     4.533      85    0.91575542   1.0373644
6     2.883      55   -0.52987412  -1.1693335

Okay! Data faithful telah siap dihidangkan untuk klasterisasi \(k\)-rerata dengan \(k=2\). Tak usah berlama-lama, mari kita mulai ke iterasi yang pertama.

Iterasi 1

Kita telah menentukan \(k=2\), sehingga algoritma tersebut selanjutnya menentukan dua titik secara acak sebagai pusat klaster-klaster awalnya. Untuk alasan demonstrasi, kita tentukan dua titik tersebut adalah \(\left( -1.4, 1 \right)\) dan \(\left( 1.4, -1 \right)\). Berikutnya, kita tentukan jarak setiap titik ke pusat klaster-klaster awal tersebut. Titik-titik yang lebih dekat ke \(\left( -1.4, 1 \right)\) berarti masuk ke “Klaster 1”, sedangkan titik-titik yang lebih dekat ke \(\left( 1.4, -1 \right)\) berarti masuk ke “Klaster 2”.

Untuk data dengan dua variabel dan \(k=2\), penentuan klaster ini juga dapat dilakukan dengan menggunakan garis yang tegak lurus dengan ruas garis yang menghubungkan dua pusat klaster tersebut dan membagi ruas garis tersebut menjadi dua sama panjang. Titik-titik data yang berada pada sisi yang sama dengan pusat klaster pertama masuk ke “Klaster 1”, sedangkan sisanya masuk ke “Klaster 2”.

Kode
faithful_1_1 <- faithful |> 
  select(eruptions_std, waiting_std) |> 
  mutate(
    d1 = (eruptions_std - (-1.4))^2 + (waiting_std - 1)^2,
    d2 = (eruptions_std - 1.4)^2 + (waiting_std - (-1))^2,
    d = if_else(d1 <= d2, d1, d2),
    klaster = if_else(d1 <= d2, "Klaster 1", "Klaster 2")
  )

head(faithful_1_1)
  eruptions_std waiting_std       d1       d2        d   klaster
1    0.09831763   0.5960248 2.408152 4.241672 2.408152 Klaster 1
2   -1.47873278  -1.2428901 5.036755 8.346098 5.036755 Klaster 1
3   -0.13561152   0.2282418 2.194289 3.866681 2.194289 Klaster 1
4   -1.05555759  -0.6544374 2.855804 6.149177 2.855804 Klaster 1
5    0.91575542   1.0373644 5.364119 4.385346 4.385346 Klaster 2
6   -0.52987412  -1.1693335 5.463127 3.753088 3.753088 Klaster 2

Agar dua klaster yang terbentuk dapat terlihat dengan jelas, mari kita visualisaskan titik-titik datanya, beserta dengan garis yang membagi titik-titik tersebut menjadi dua klaster. Perhatikan Gambar 6!

Kode
plot_1_1 <- faithful_1_1 |> 
  ggplot() + 
  geom_point(
    aes(
      x = eruptions_std,
      y = waiting_std,
      color = klaster
    )
  ) + 
  geom_point(
    data = tibble(
      x = c(-1.4, 1.4),
      y = c(1, -1),
      klaster = c("Klaster 1", "Klaster 2")
    ),
    aes(x, y),
    shape = 4,
    size = 5,
    stroke = 3,
    color = "white"
  ) + 
  geom_point(
    data = tibble(
      x = c(-1.4, 1.4),
      y = c(1, -1),
      klaster = c("Klaster 1", "Klaster 2")
    ),
    aes(x, y, color = klaster),
    shape = 4,
    size = 5,
    stroke = 1.5
  ) + 
  geom_abline(
    slope = 7/5,
    intercept = 0,
    color = "#00BA38"
  ) + 
  theme_minimal() + 
  theme(
    legend.position = "none"
  )

plot_1_1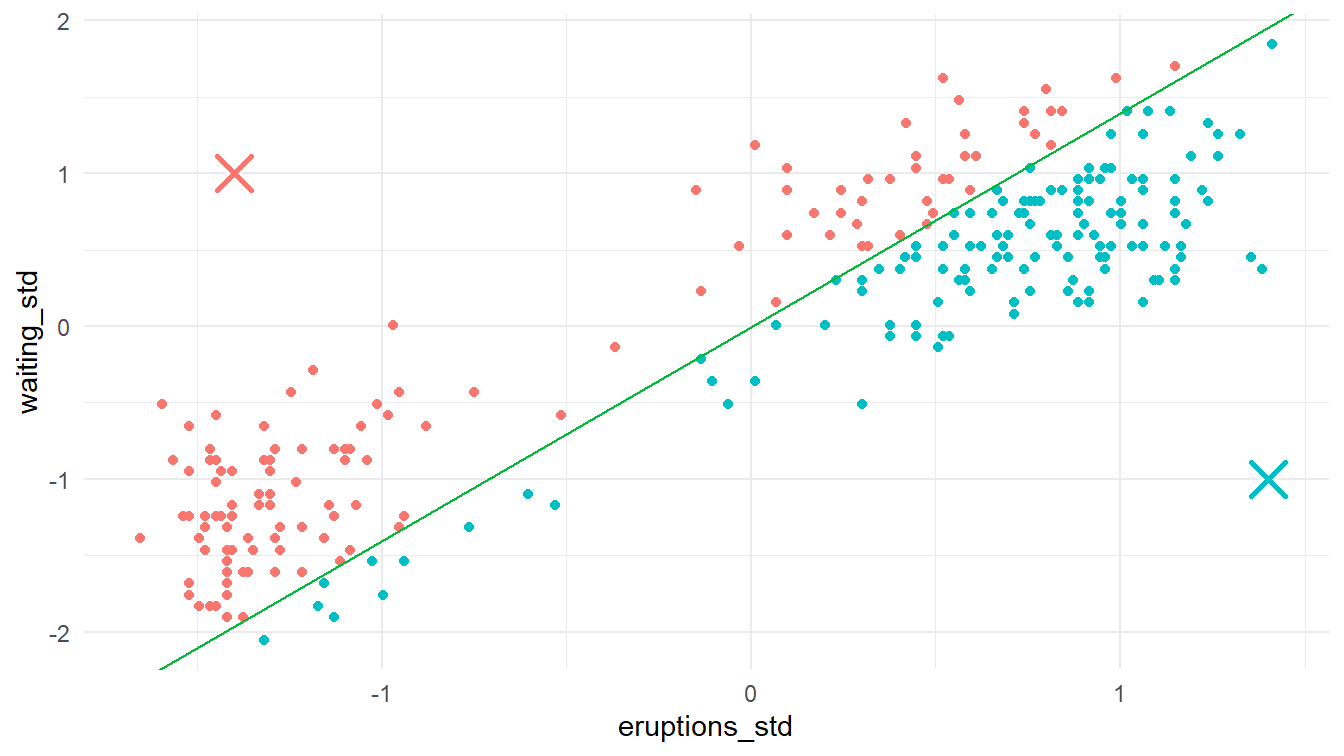
Gambar 6: Klaster-klaster yang terbentuk pada langkah pertama dalam iterasi pertama (Iterasi 1-1)

Langkah kedua di iterasi pertama adalah menentukan pusat masing-masing klaster dengan cara menentukan reratanya.

Kode
pusat_klaster_1_2 <- faithful_1_1 |> 
  group_by(klaster) |> 
  summarise(
    x = mean(eruptions_std),
    y = mean(waiting_std)
  )

pusat_klaster_1_2
# A tibble: 2 × 3
  klaster        x      y
  <chr>      <dbl>  <dbl>
1 Klaster 1 -0.730 -0.449
2 Klaster 2  0.678  0.418

Selanjutnya, kita plot pusat klaster-klaster yang baru tersebut ke diagram pencar sebelumnya, menggantikan pusat-pusat klaster yang lama. Hasilnya disajikan pada Gambar 7.

Kode
# Menyiapkan data `faithful_1_2`
faithful_1_2 <- faithful_1_1 |> 
  select(eruptions_std, waiting_std, klaster) |> 
  mutate(
    d1 = (eruptions_std - pusat_klaster_1_2[[1,2]])^2 + (waiting_std - pusat_klaster_1_2[[1,3]])^2,
    d2 = (eruptions_std - pusat_klaster_1_2[[2,2]])^2 + (waiting_std - pusat_klaster_1_2[[2,3]])^2,
    d = if_else(klaster == "Klaster 1", d1, d2)
  )

# Plot Iterasi 1-2
plot_1_2 <- faithful_1_2 |> 
  ggplot() + 
  geom_point(
    aes(
      x = eruptions_std,
      y = waiting_std,
      color = klaster
    )
  ) + 
  geom_point(
    data = pusat_klaster_1_2,
    aes(
      x = x,
      y = y
    ),
    shape = 4,
    size = 5,
    stroke = 3,
    color = "white"
  ) + 
  geom_point(
    data = pusat_klaster_1_2,
    aes(
      x = x,
      y = y,
      color = klaster
    ),
    shape = 4,
    size = 5,
    stroke = 1.5
  ) + 
  theme_minimal() + 
  theme(
    legend.position = "none"
  )

plot_1_2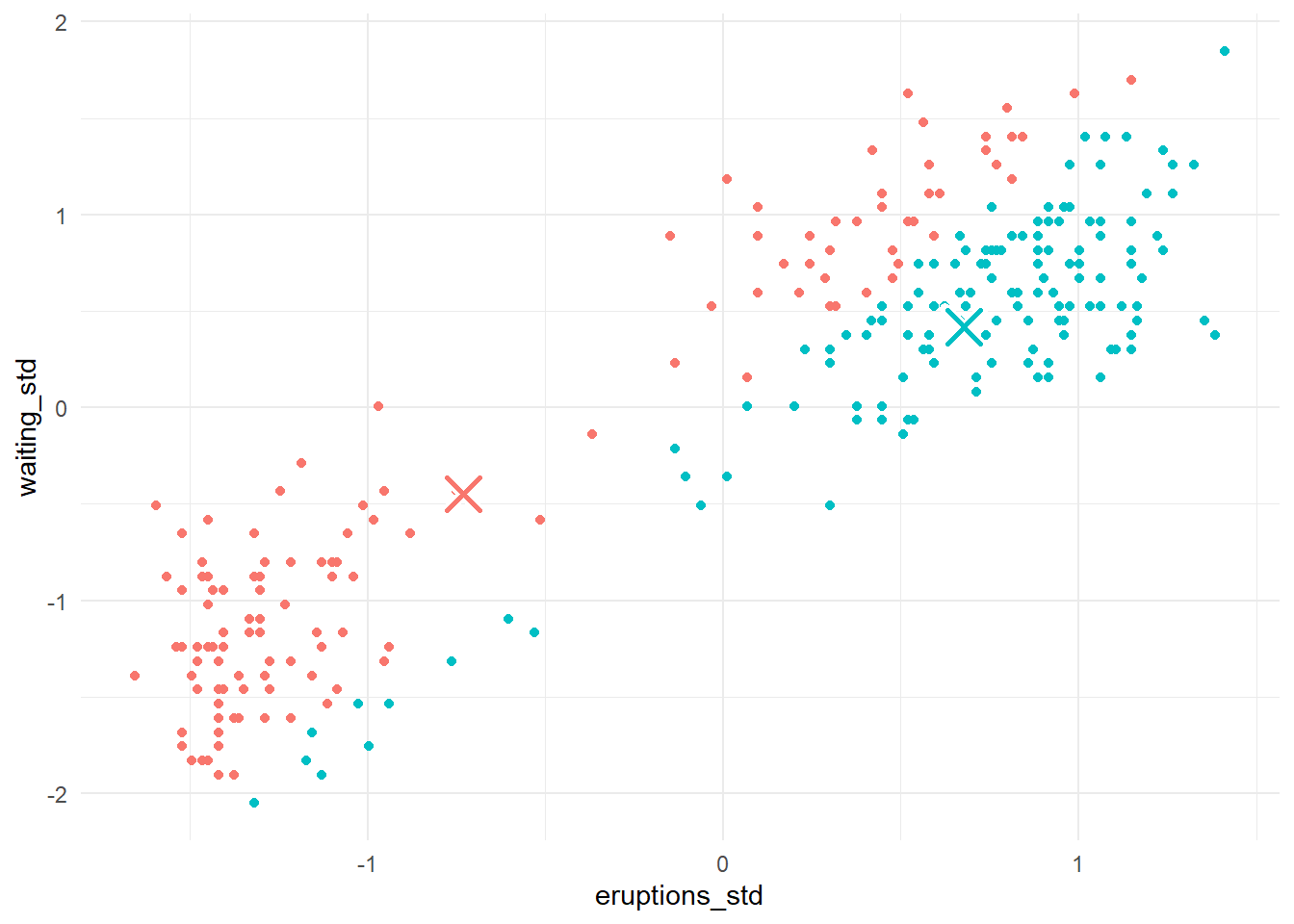
Gambar 7: Pusat dua klaster pada langkah kedua dalam iterasi pertama (Iterasi 1-2)

Iterasi pertama telah selesai dilakukan. Sekarang kita lanjut ke Bagian 3.2.

Iterasi 2

Kita masuk ke iterasi yang kedua. Pada langkah pertama, kita gunakan pusat klaster-klaster sebelumnya untuk memasukkan titik-titik datanya ke klasternya masing-masing.

Kode
faithful_2_1 <- faithful_1_2 |> 
  select(-d, -klaster) |> 
  mutate(
    d = if_else(d1 <= d2, d1, d2),
    klaster = if_else(d1 <= d2, "Klaster 1", "Klaster 2")
  )

head(faithful_2_1)
  eruptions_std waiting_std        d1        d2         d   klaster
1    0.09831763   0.5960248 1.7796010 0.3683804 0.3683804 Klaster 2
2   -1.47873278  -1.2428901 1.1897322 7.4106840 1.1897322 Klaster 1
3   -0.13561152   0.2282418 0.8128978 0.6985503 0.6985503 Klaster 2
4   -1.05555759  -0.6544374 0.1478379 4.1560559 0.1478379 Klaster 1
5    0.91575542   1.0373644 4.9200217 0.4404101 0.4404101 Klaster 2
6   -0.52987412  -1.1693335 0.5583201 3.9784302 0.5583201 Klaster 1

Kita visualisasikan titik-titik data dalam faithful beserta dengan klaster-klaster yang telah dihasilkan. Perhatikan Gambar 8!

Kode
plot_2_1 <- faithful_2_1 |> 
  ggplot() + 
  geom_point(
    aes(
      x = eruptions_std,
      y = waiting_std,
      color = klaster
    )
  ) + 
  geom_point(
    data = pusat_klaster_1_2,
    aes(
      x = x,
      y = y
    ),
    shape = 4,
    size = 5,
    stroke = 2,
    color = "white"
  ) + 
  geom_point(
    data = pusat_klaster_1_2,
    aes(
      x = x,
      y = y,
      color = klaster
    ),
    shape = 4,
    size = 5,
    stroke = 1.5
  ) + 
  geom_abline(
    slope = -1.624589,
    intercept = -0.058,
    color = "#00BA38"
  ) + 
  theme_minimal() + 
  theme(
    legend.position = "none"
  )

plot_2_1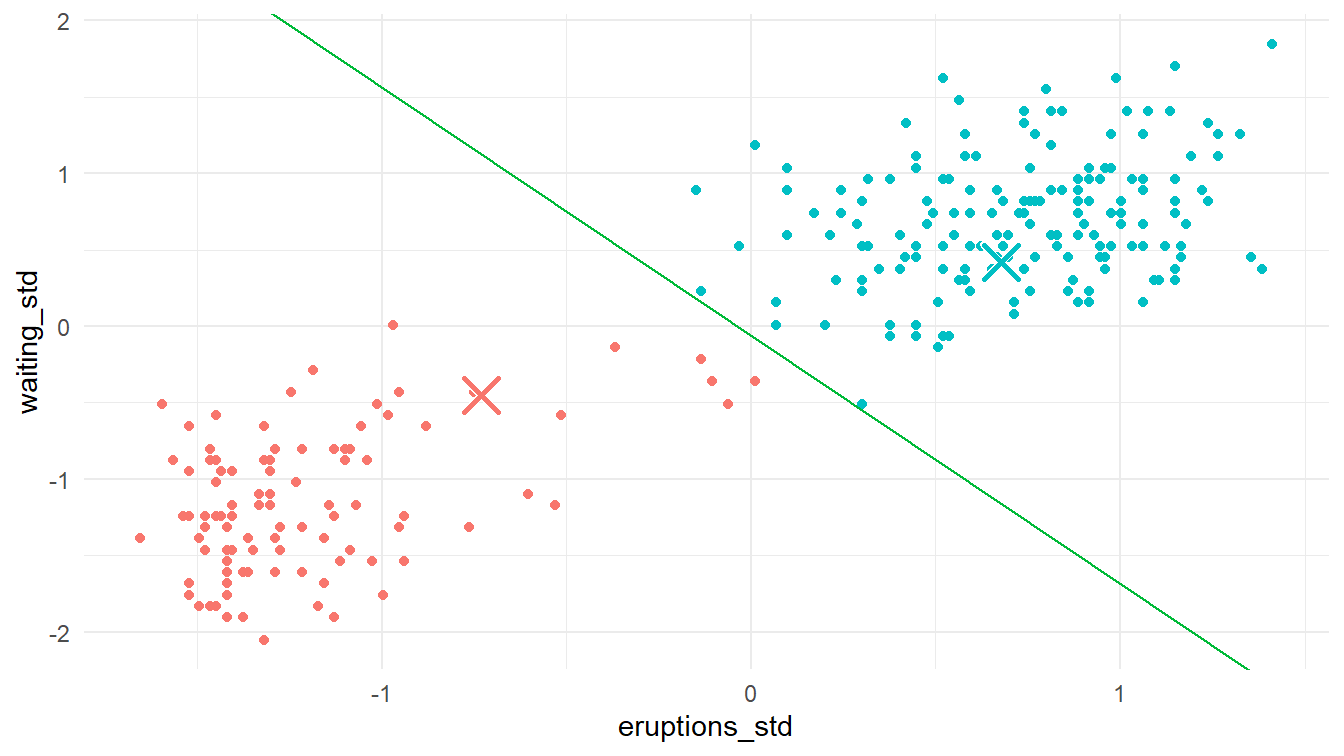
Gambar 8: Klaster-klaster yang terbentuk pada langkah pertama dalam iterasi kedua (Iterasi 2-1)

Berikutnya, kita tentukan pusat klaster-klaster yang baru. Caranya sama, yaitu kita tentukan rerata semua titik pada masing-masing klaster.

Kode
pusat_klaster_2_2 <- 
  faithful_2_1 |> 
  group_by(klaster) |> 
  summarise(
    x = mean(eruptions_std),
    y = mean(waiting_std)
  )

pusat_klaster_2_2
# A tibble: 2 × 3
  klaster        x      y
  <chr>      <dbl>  <dbl>
1 Klaster 1 -1.21  -1.16 
2 Klaster 2  0.729  0.698

Apa selanjutnya? Kita plot pusat-pusat klaster yang baru beserta dengan titik-titik datanya. Hasilnya disajikan pada Gambar 9.

Kode
# Mempersiapkan `faithful_2_2`
faithful_2_2 <- faithful_2_1 |> 
  select(eruptions_std, waiting_std, klaster) |> 
  mutate(
    d1 = (eruptions_std - pusat_klaster_2_2[[1,2]])^2 + (waiting_std - pusat_klaster_2_2[[1,3]])^2,
    d2 = (eruptions_std - pusat_klaster_2_2[[2,2]])^2 + (waiting_std - pusat_klaster_2_2[[2,3]])^2,
    d = if_else(klaster == "Klaster 1", d1, d2)
  )

# Plot Iterasi 2-2
plot_2_2 <- faithful_2_2 |> 
  ggplot() + 
  geom_point(
    aes(
      x = eruptions_std,
      y = waiting_std,
      color = klaster
    )
  ) + 
  geom_point(
    data = pusat_klaster_2_2,
    aes(
      x = x,
      y = y
    ),
    shape = 4,
    size = 5,
    stroke = 3,
    color = "white"
  ) + 
  geom_point(
    data = pusat_klaster_2_2,
    aes(
      x = x,
      y = y,
      color = klaster
    ),
    shape = 4,
    size = 5,
    stroke = 1.5,
  ) + 
  theme_minimal() + 
  theme(
    legend.position = "none"
  )

plot_2_2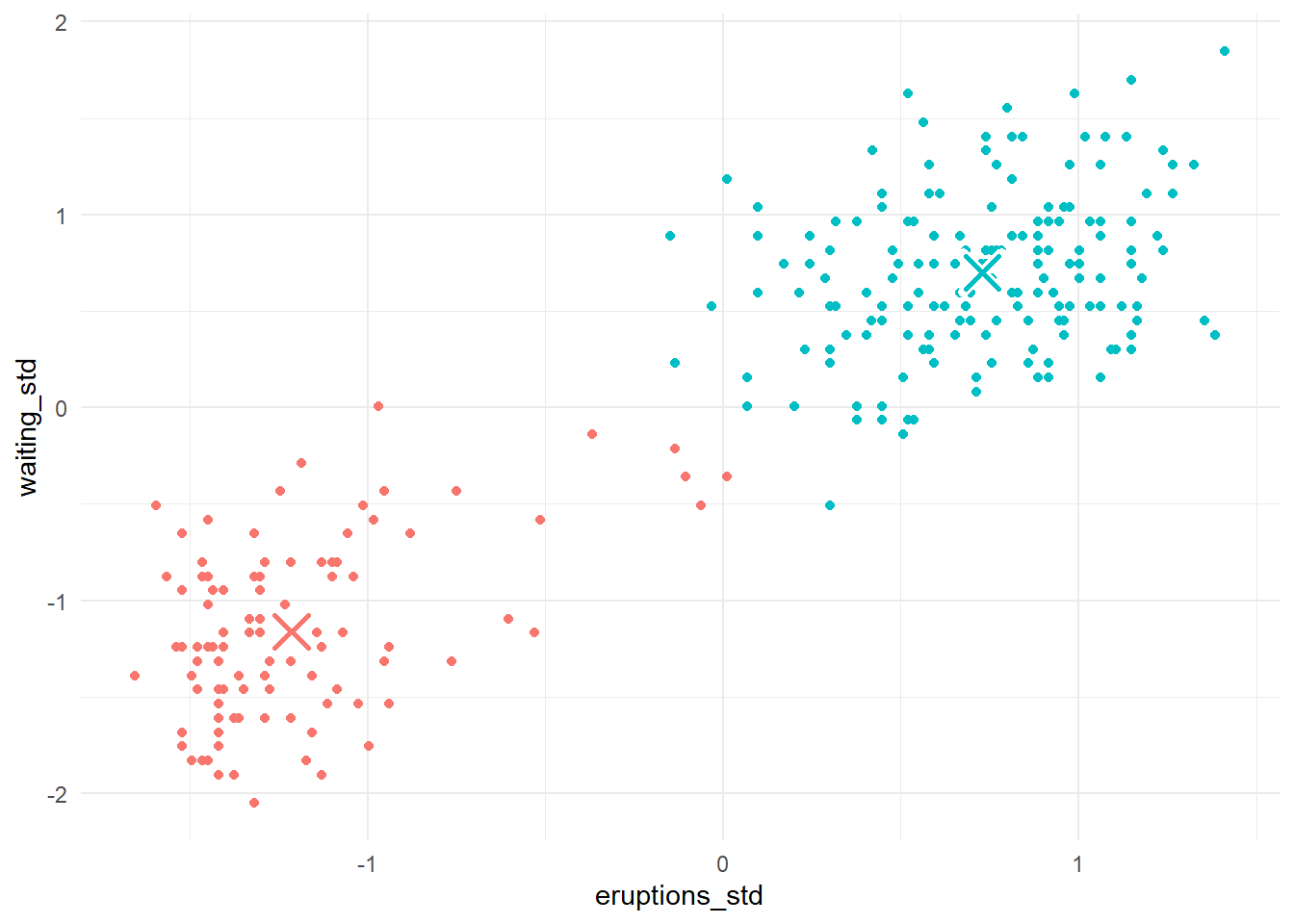
Gambar 9: Pusat-pusat klaster pada langkah kedua dalam iterasi kedua (Iterasi 2-2)

Mari kita lanjut ke iterasi berikutnya, Bagian 3.3.

Iterasi 3

Pada langkah pertama di iterasi ketiga, kita pasangkan setiap titik ke dalam klasternya masing-masing berdasarkan jaraknya terhadap pusat klaster-klaster yang baru.

Kode
faithful_3_1 <- faithful_2_2 |> 
  select(-d, -klaster) |> 
  mutate(
    d = if_else(d1 <= d2, d1, d2),
    klaster = if_else(d1 <= d2, "Klaster 1", "Klaster 2")
  )

head(faithful_3_1)
  eruptions_std waiting_std         d1        d2          d   klaster
1    0.09831763   0.5960248 4.81663204 0.4075842 0.40758421 Klaster 2
2   -1.47873278  -1.2428901 0.07632207 8.6381936 0.07632207 Klaster 1
3   -0.13561152   0.2282418 3.09872776 0.9672434 0.96724344 Klaster 2
4   -1.05555759  -0.6544374 0.28368178 5.0114795 0.28368178 Klaster 1
5    0.91575542   1.0373644 9.37813119 0.1503982 0.15039817 Klaster 2
6   -0.52987412  -1.1693335 0.46850713 5.0695722 0.46850713 Klaster 1

Selanjutnya kita plot titik-titik yang telah masuk ke dalam klasternya masing-masing dengan menggunakan diagram pencar. Perhatikan Gambar 10!

Kode
plot_3_1 <- faithful_3_1 |> 
  ggplot() + 
  geom_point(
    aes(
      x = eruptions_std,
      y = waiting_std,
      color = klaster
    )
  ) + 
  geom_point(
    data = pusat_klaster_2_2,
    aes(
      x = x,
      y = y
    ),
    shape = 4,
    size = 5,
    stroke = 3,
    color = "white"
  ) + 
  geom_point(
    data = pusat_klaster_2_2,
    aes(
      x = x,
      y = y,
      color = klaster
    ),
    shape = 4,
    size = 5,
    stroke = 1.5
  ) + 
  geom_abline(
    slope = -1.0436,
    intercept = -0.486595,
    color = "#00BA38"
  ) + 
  theme_minimal() + 
  theme(
    legend.position = "none"
  )

plot_3_1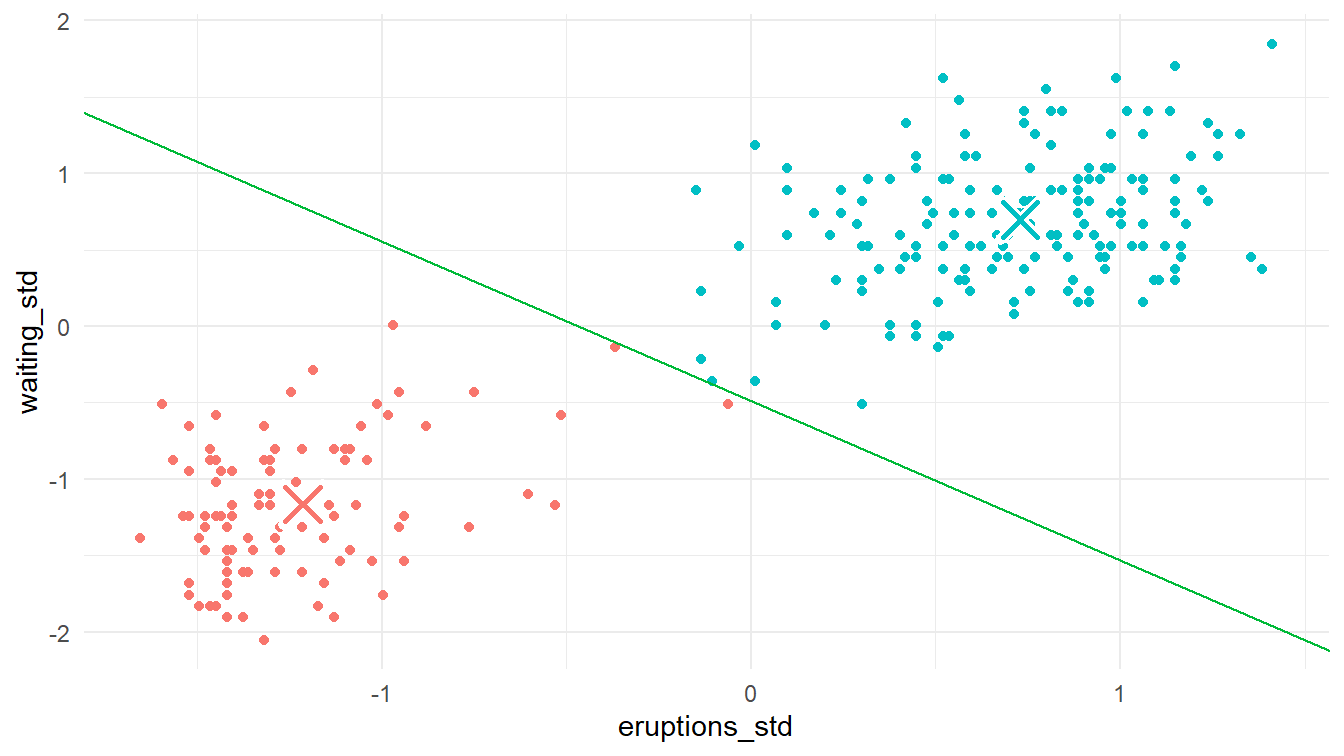
Gambar 10: Klaster-klaster yang terbentuk pada langkah pertama dalam iterasi ketiga (Iterasi 3-1)

Pada langkah kedua, kita tentukan pusat-pusat klaster yang baru. Caranya adalah sebagai berikut.

Kode
pusat_klaster_3_2 <- faithful_3_1 |> 
  group_by(klaster) |> 
  summarise(
    x = mean(eruptions_std),
    y = mean(waiting_std)
  )

pusat_klaster_3_2
# A tibble: 2 × 3
  klaster        x      y
  <chr>      <dbl>  <dbl>
1 Klaster 1 -1.25  -1.19 
2 Klaster 2  0.715  0.680

Kita plot pusat klaster-klaster yang baru tersebut bersama dengan titik-titik data sebelumnya. Perhatikan Gambar 11!

Kode
# Mempersiapkan `faithful_3_2`
faithful_3_2 <- faithful_3_1 |> 
  select(eruptions_std, waiting_std, klaster) |> 
  mutate(
    d1 = (eruptions_std - pusat_klaster_3_2[[1,2]])^2 + (waiting_std - pusat_klaster_3_2[[1,3]])^2,
    d2 = (eruptions_std - pusat_klaster_3_2[[2,2]])^2 + (waiting_std - pusat_klaster_3_2[[2,3]])^2,
    d = if_else(klaster == "Klaster 1", d1, d2)
  )

# Plot Iterasi 3-2
plot_3_2 <- faithful_3_2 |> 
  ggplot() + 
  geom_point(
    aes(
      x = eruptions_std,
      y = waiting_std,
      color = klaster
    )
  ) + 
  geom_point(
    data = pusat_klaster_3_2,
    aes(
      x = x,
      y = y
    ),
    shape = 4,
    size = 5,
    stroke = 3,
    color = "white"
  ) + 
  geom_point(
    data = pusat_klaster_3_2,
    aes(
      x = x,
      y = y,
      color = klaster
    ),
    shape = 4,
    size = 5,
    stroke = 1.5,
  ) +
  theme_minimal() + 
  theme(
    legend.position = "none"
  )

plot_3_2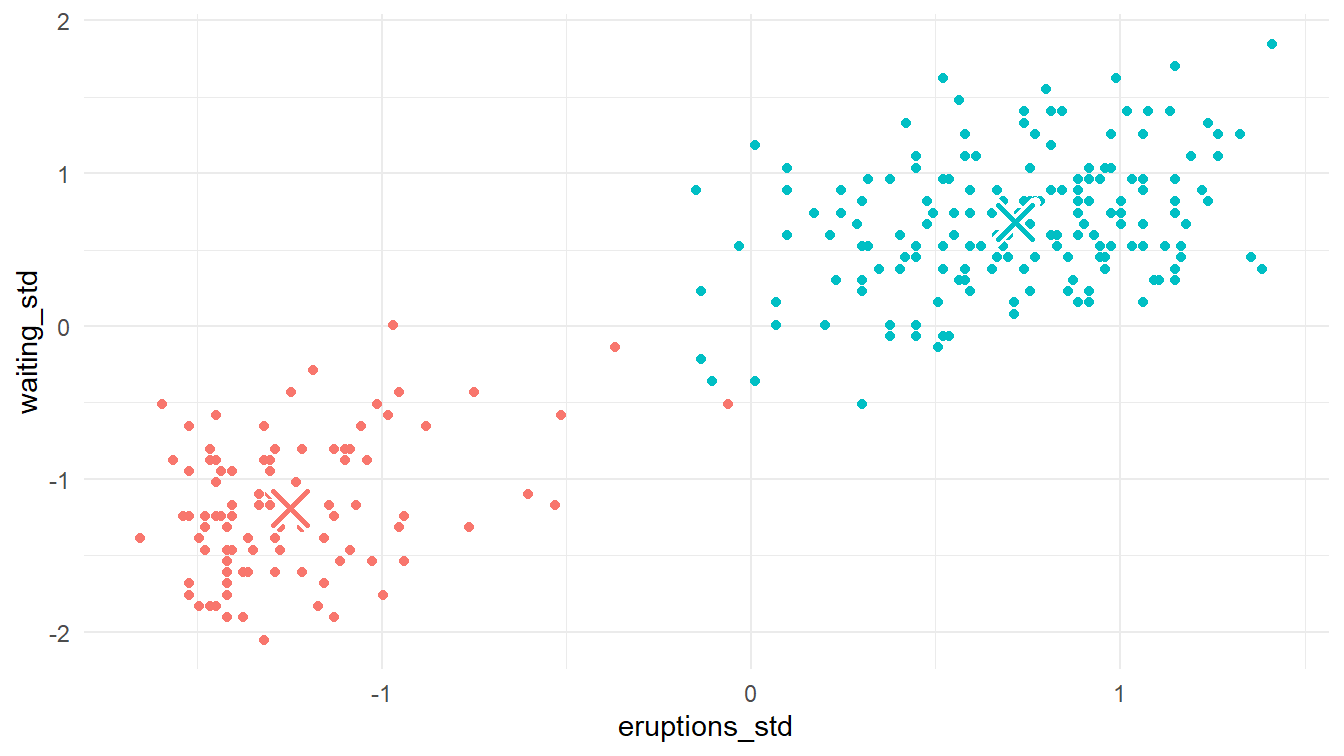
Gambar 11: Pusat-pusat klaster pada langkah kedua dalam iterasi ketiga (Iterasi 2-2)

Kita telah menyelesaikan langkah kedua dalam iterasi ketiga. Sekarang, mari kita lanjut ke iterasi berikutnya!

Iterasi 4

Apa langkah pertama di iterasi keempat ini? Ya! Kita masukkan setiap titik ke dalam klasternya berdasarkan jaraknya ke pusat klaster-klaster yang terakhir.

Kode
faithful_4_1 <- faithful_3_2 |> 
  select(-d, -klaster) |> 
  mutate(
    d = if_else(d1 <= d2, d1, d2),
    klaster = if_else(d1 <= d2, "Klaster 1", "Klaster 2")
  )

head(faithful_4_1)
  eruptions_std waiting_std         d1        d2          d   klaster
1    0.09831763   0.5960248 4.99975759 0.3869199 0.38691994 Klaster 2
2   -1.47873278  -1.2428901 0.05581732 8.5091284 0.05581732 Klaster 1
3   -0.13561152   0.2282418 3.24674404 0.9271753 0.92717528 Klaster 2
4   -1.05555759  -0.6544374 0.32272192 4.9148263 0.32272192 Klaster 1
5    0.91575542   1.0373644 9.64038624 0.1680127 0.16801271 Klaster 2
6   -0.52987412  -1.1693335 0.51720760 4.9695885 0.51720760 Klaster 1

Sekarang setiap titik telah memiliki klasternya masing-masing. Kita plot titik-titik tersebut ke dalam diagram pencar. Perhatikan Gambar 12!

Kode
plot_4_1 <- faithful_4_1 |> 
  ggplot() + 
  geom_point(
    aes(
      x = eruptions_std,
      y = waiting_std,
      color = klaster
    )
  ) + 
  geom_point(
    data = pusat_klaster_3_2,
    aes(
      x = x,
      y = y
    ),
    shape = 4,
    size = 5,
    stroke = 3,
    color = "white"
  ) + 
  geom_point(
    data = pusat_klaster_3_2,
    aes(
      x = x,
      y = y,
      color = klaster
    ),
    shape = 4,
    size = 5,
    stroke = 1.5
  ) + 
  geom_abline(
    slope = -1.0508,
    intercept = -0.534564,
    color = "#00BA38"
  ) + 
  theme_minimal() + 
  theme(
    legend.position = "none"
  )

plot_4_1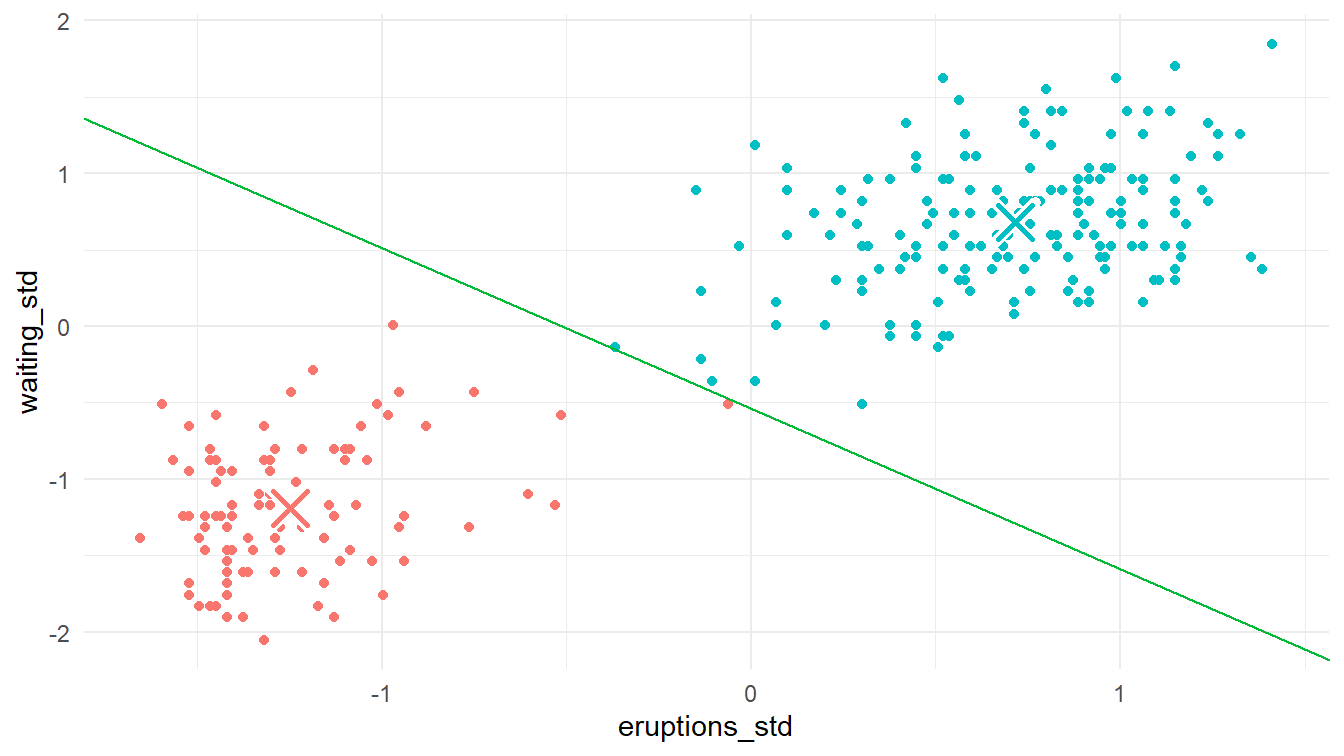
Gambar 12: Klaster-klaster yang terbentuk pada langkah pertama dalam iterasi keempat (Iterasi 4-1)

Kita lanjut ke langkah kedua. Di langkah kedua ini, kita cari pusat klaster-klasternya yang baru.

pusat_klaster_4_2 <- faithful_4_1 |> 
  group_by(klaster) |> 
  summarise(
    x = mean(eruptions_std),
    y = mean(waiting_std),
    .groups = "drop"
  )

pusat_klaster_4_2
# A tibble: 2 × 3
  klaster        x      y
  <chr>      <dbl>  <dbl>
1 Klaster 1 -1.26  -1.20 
2 Klaster 2  0.708  0.675

Berikutnya, kita plot pusat-pusat klaster yang baru tersebut bersama dengan titik-titik datanya. Perhatikan gambar berikut!

Kode
# Mempersiapkan `faithful_4_2`
faithful_4_2 <- faithful_4_1 |> 
  select(eruptions_std, waiting_std, klaster) |> 
  mutate(
    d1 = (eruptions_std - pusat_klaster_4_2[[1,2]])^2 + (waiting_std - pusat_klaster_4_2[[1,3]])^2,
    d2 = (eruptions_std - pusat_klaster_4_2[[2,2]])^2 + (waiting_std - pusat_klaster_4_2[[2,3]])^2,
    d = if_else(klaster == "Klaster 1", d1, d2)
  )

# Plot Iterasi 4-2
plot_4_2 <- faithful_4_2 |> 
  ggplot() + 
  geom_point(
    aes(
      x = eruptions_std,
      y = waiting_std,
      color = klaster
    )
  ) + 
  geom_point(
    data = pusat_klaster_4_2,
    aes(
      x = x,
      y = y
    ),
    shape = 4,
    size = 5,
    stroke = 3,
    color = "white"
  ) + 
  geom_point(
    data = pusat_klaster_4_2,
    aes(
      x = x,
      y = y,
      color = klaster
    ),
    shape = 4,
    size = 5,
    stroke = 1.5,
  ) +
  theme_minimal() + 
  theme(
    legend.position = "none"
  )

plot_4_2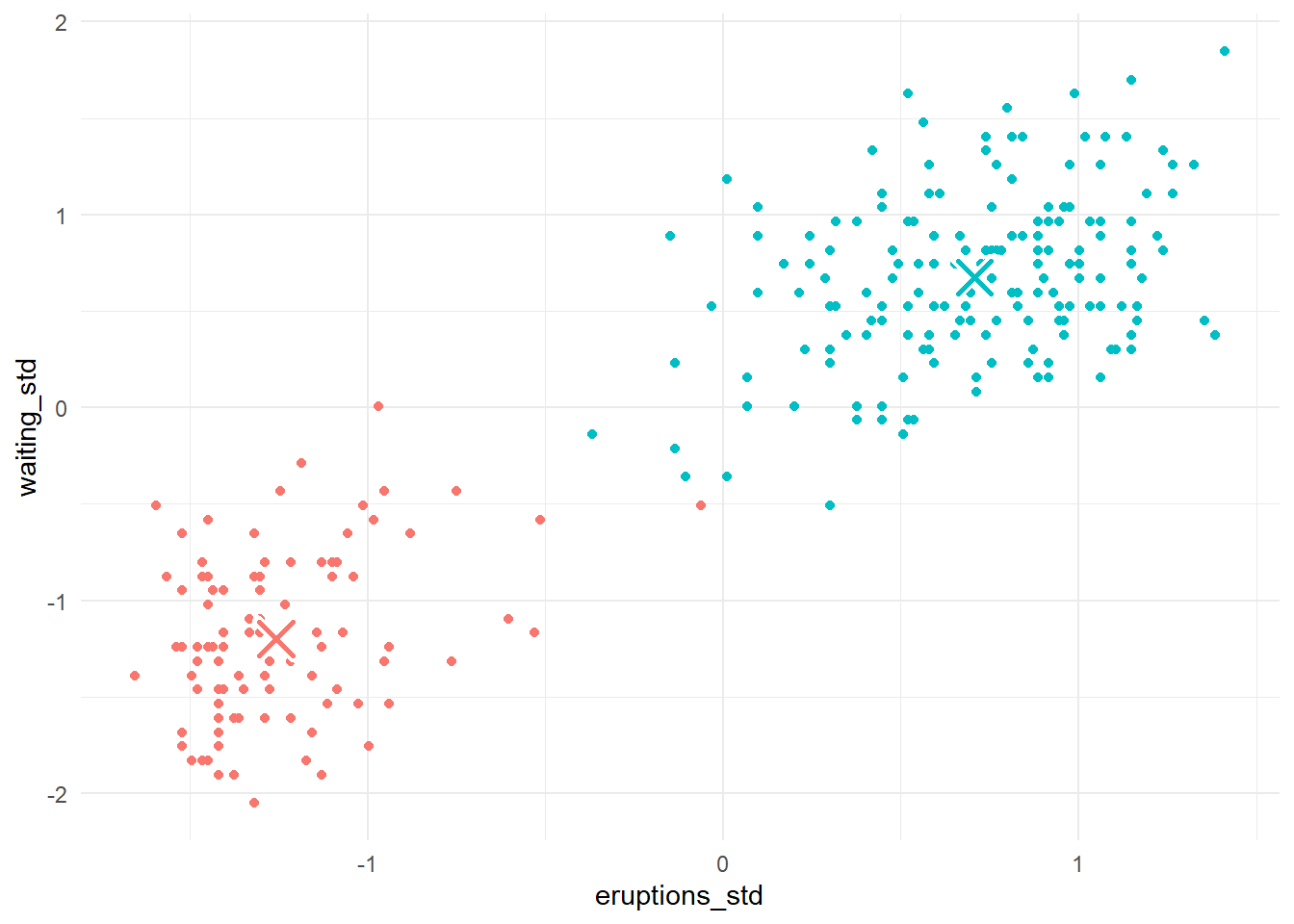
Gambar 13: Pusat-pusat klaster pada langkah kedua dalam iterasi keempat (Iterasi 4-2)

Kilas Balik

Sampai di sini, kita telah melakukan empat kali iterasi. Apakah kita perlu melakukan iterasi lagi? Ataukah iterasinya sudah cukup? Untuk menjawab pertanyaan-pertanyaan tersebut, kita dapat menggunakan \(WCSS\) (Within-Cluster Sum of Squares) atau jumlah kuadrat jarak setiap titik ke pusat klasternya. Dengan demikian, \(WCSS\) ditentukan dengan Persamaan 1.

\[ WCSS=\sum_{j=1}^{k}\sum_{x_{i}\in C_{j}}^{}\left\| x_{i}-p_{j}\right\|^2 \tag{1}\]

  • \(C_{j}\) adalah klaster ke-\(j\).

  • \(x_{i}\) adalah sebuah titik data dalam klaster \(C_{j}\).

  • \(p_{j}\) adalah pusat klaster (centroid) dari \(C_{j}\).

  • \(\left\| x_{i} - p_{j} \right\|^2\) adalah kuadrat jarak antara titik data dan pusat klasternya.

Dengan rumus ini, kita dapat menentukan \(WCSS\) pada langkah pertama dalam iterasi pertama sebagai berikut.

Kode
wcss_1_1 <- faithful_1_1 |> 
  summarise(
    wcss = sum(d)
  )

wcss_1_1
      wcss
1 1046.952

Dengan cara yang serupa, kita dapat menentukan \(WCSS\) untuk langkah pertama dan kedua dalam semua iterasi. Kita simpan nilai-nilai \(WCSS\) tersebut ke dalam wcss_df.

Kode
daftar_faithful <- list(
  "1_1" = faithful_1_1,
  "1_2" = faithful_1_2,
  "2_1" = faithful_2_1,
  "2_2" = faithful_2_2,
  "3_1" = faithful_3_1,
  "3_2" = faithful_3_2,
  "4_1" = faithful_4_1,
  "4_2" = faithful_4_2
)

wcss_df <- map_dfr(
  daftar_faithful,
  ~ summarise(.x, wcss = sum(d)),
  .id = "faithful"
) |> 
  mutate(
    iterasi = seq(from = 0.5, to = 4, by = 0.5),
    group = as_factor(rep(c("M", "E"), 4))
  )

wcss_df
  faithful       wcss iterasi group
1      1_1 1046.95159     0.5     M
2      1_2  356.18666     1.0     E
3      2_1  170.24221     1.5     M
4      2_2   80.67025     2.0     E
5      3_1   79.61314     2.5     M
6      3_2   79.34288     3.0     E
7      4_1   79.31314     3.5     M
8      4_2   79.28340     4.0     E

Kita telah memiliki untuk setiap langkahnya dalam wcss_df. Sekarang, kita dapat melihat tren nilai \(WCSS\) tersebut. Perhatikan Gambar 14!

Kode
wcss_df |> 
  ggplot(aes(x = iterasi, y = wcss)) + 
  geom_line(
    col = "#00BA38",
    linewidth = 1
  ) + 
  geom_point(
    aes(col = group),
    shape = 1,
    size = 3,
    stroke = 1.5
  ) + 
  theme_minimal() + 
  theme(
    legend.position = "none"
  )
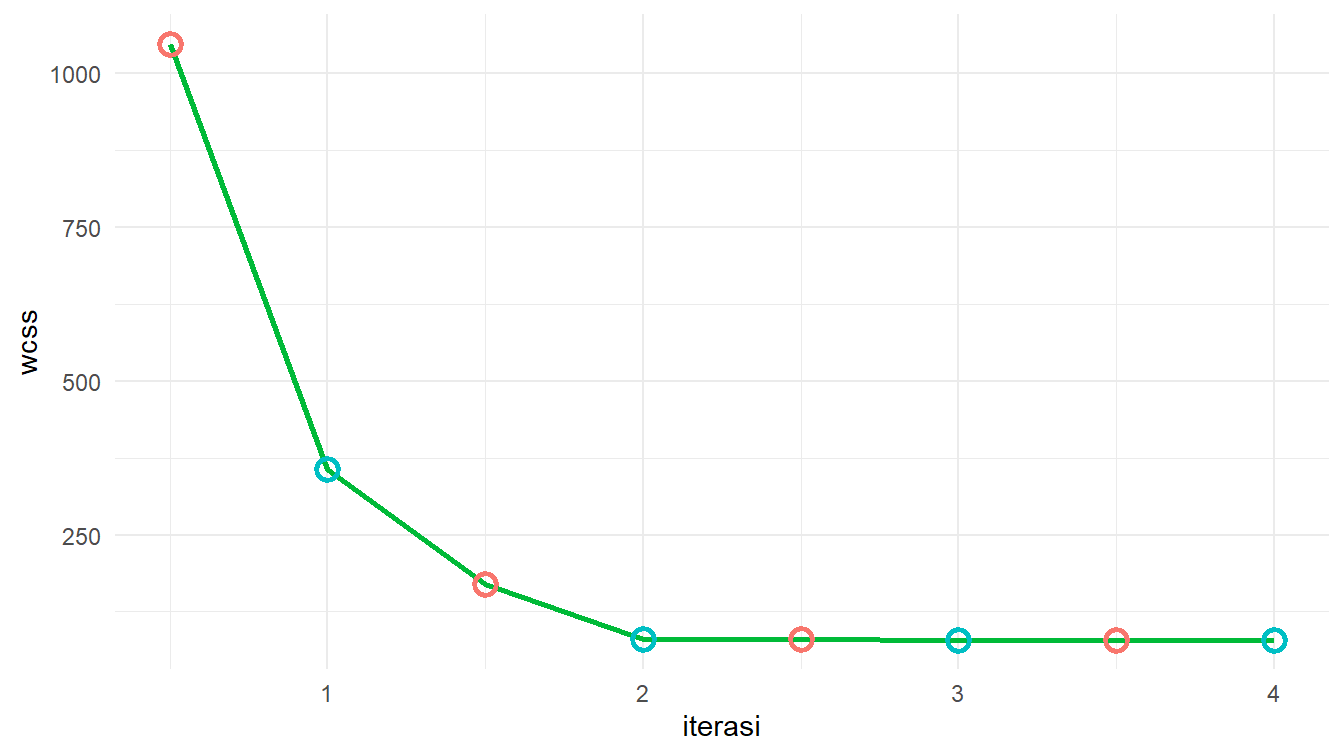
Gambar 14: Tren nilai WCSS dari langkah pertama iterasi pertama sampai langkah kedua iterasi keempat

Berdasarkan Gambar 14, kita dapat melihat bahwa nilai \(WCSS\) sudah konvergen pada iterasi kedua. Bahkan, dari iterasi ketiga sampai keempat, perubahan anggota kluster sudah tidak signifikan. Oleh karena itu, iterasinya kita cukupkan sampai iterasi keempat. Untuk melihat kembali apa yang telah kita lakukan mulai iterasi pertama sampai keempat, perhatikan Gambar 15!

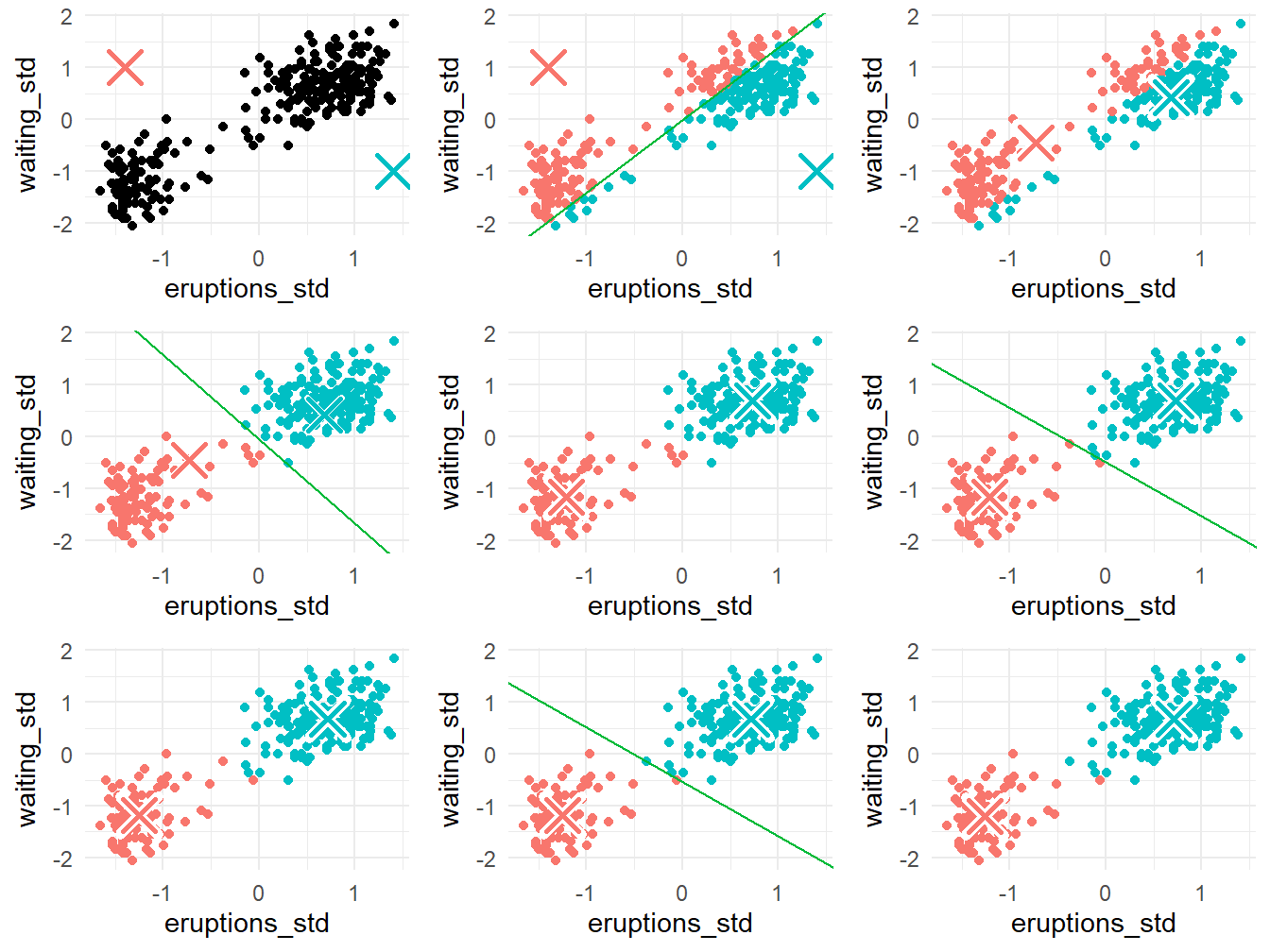
Gambar 15: Empat iterasi klasterasisasi k-rerata terhadap data faithful yang dinormalbakukan.

Klasterisasi \(K\)-Rerata dengan Fungsi kmeans()

Pada Bagian 3, kita telah melakukan klasterisasi \(k\)-rerata langkah demi langkah, dari iterasi pertama sampai keempat. Banyak hal yang telah kita lakukan. Apakah ada fungsi di R yang dapat melakukan klasterisasi \(k\)-rerata secara otomatis dan cepat? Tentu saja ada! Fungsi itu adalah kmeans().

Untuk membagi data kita sebelumnya, yaitu faithful, menjadi \(k=2\) klaster, kita gunakan kode berikut.

Kode
# Menyiapkan dataframe untuk `kmeans()`
faithful_std <- faithful |> 
  select(eruptions_std, waiting_std)

# Menerapkan `kmeans()`
cl <- kmeans(x = faithful_std, centers = 2)

# Memasukkan klaster yang dihasilkan ke dalam `faithful`
faithful <- faithful |> 
  mutate(
    klaster = cl$cluster
  )

Ingin tahu bagaimana hasilnya? Mari kita plot diagram pencar data faithful. Perhatikan Gambar 16!

Kode
faithful |> 
  mutate(
    klaster = as_factor(3 - klaster)
  ) |> 
  ggplot(
    aes(x = eruptions_std, y = waiting_std, color = klaster)
  ) + 
  geom_point() + 
  theme_minimal() + 
  theme(
    legend.position = "none"
  )
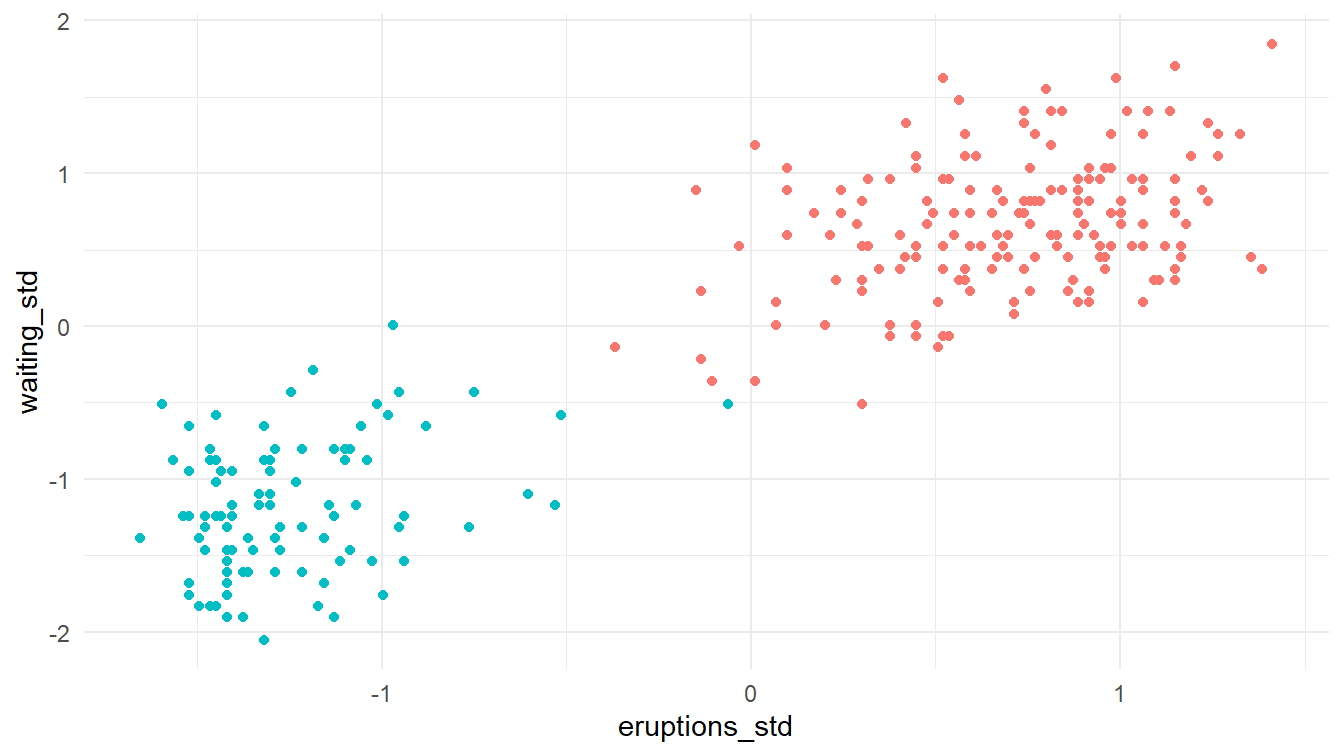
Gambar 16: Klaster-klaster dalam data faithful hasil klasterisasi k-rerata dengan fungsi kmeans()

Apakah Gambar 16 sama dengan Gambar 13? Ternyata sama hasilnya.

Catatan Akhir

Kita telah mempelajari klasterisasi \(k\)-rerata. Mengapa kita perlu mempelajari metode ini? Jawabannya telah kita pelajari pada Bagian 1. Setelah itu, bagaimana kerja algoritma \(k\)-rerata juga telah kita bahas di Bagian 2. Langkah-langkah rinci algoritma tersebut telah diilustrasikan pada Bagian 3. Tak hanya itu, Bagian 4 juga memberikan jalan cepat dengan fungsi kmeans().

Sekarang, kita kembali ke permasalahan awal. Bagian awal artikel ini menyebutkan bahwa klasterisasi \(k\)-means dapat digunakan untuk memanipulasi gambar sehingga menghasilkan Gambar 1. Bagaimana caranya? Tutorial selengkapnya dapat ditemukan pada pos berikutnya!

Kembali ke atas

Penggunaan Kembali